Statistical Mechanics

Large Numbers

Intensive: $O (N^{0}) = O (1)$ .

Extensive: $O (N^{1}) = O (N)$ . Note: Ext/Ext = Int, Int x Ext = Ext.

Exponentially Large: $O (e^{N})$ .

How many microstates in a simple system. Consider a site with 2 states or a 4x4 grid, $N = N_{s}^{2} = 4^{2} = 16$ .

Ising model, $s_{i} = {- 1, + 1}$ .

In the 4x4 grid, we have $2^{16} = 65536$ states. An exaflop is $10^{18}$ floating point operations per second which is roughly $2^{60}$ .

Estimate, 1000 Exaflops total in the world, $2^{10}$ .

30 million seconds, $3 \cdot 10^{7}$ . Then, $2^{2} 5$ . So, $2^{95}$ sites can be calculated in a year. If we double in a year, we can calculate one more site.

Roughly, $2^{80}$ atoms in the universe.

$S = \sum_{α} \exp (\frac{E_{α}}{k T})$ , $E_{α} = \sum_{i = 1}^{N} ϵ_{i}$ .

$S = \sum_{α = 1}^{N^{P}} Y_{α}$ , $0 \leq Y_{α} \sim O (\exp (N ϕ_{α}))$ . We can choose it to be bounded below by any number we choose, but zero is typically most convenient. Then, $0 \leq Y_{α} \leq Y_{m} a x$ .

So, $y_{m a x} \leq S \leq N^{P} y_{m a x}$ .

Consider, $\frac{\ln S}{N}$ . Then, $\frac{\ln y_{m a x}}{N} \leq \frac{\ln S}{N} \leq \frac{p \ln N}{N} + \frac{\ln y_{m a x}}{N}$ . As $N \to \infty$ , $\ln N / N \to 0$ , so $\frac{\ln S}{N} \approx \frac{\ln y_{m a x}}{N}$ , hence $\ln S \approx \ln y_{m a x}$ .

Integrals

$I = \int d x \exp (N ϕ (x))$ . Approximating these by the maximum value of integrand (φ(x_max)) obtained at $x = x_{m a x}$ .

Taylor expanding around this point, $J \approx \int d x \exp (N (ϕ (x_{m a x}) + \frac{1}{2} ϕ (x - x_{m a x})^{2} + \dots))$ . $ϕ^{'} (x_{m a x}) = 0, ϕ^{″} (x_{m a x}) < 0$ due to $x$ being a maxiumum.

$J \approx \exp (N ϕ (x_{m a x})) \int d x \exp (- \frac{N}{2} | ϕ^{″} (x_{m a x}) | (x - x_{m a x})^{2}) = \sqrt{\frac{2 π}{N / ϕ^{″} (x_{m a x})}} \exp (N ϕ (x_{m a x}))$ .

2 major corrections are needed:

Higher order terms: powers of 1/N
Other local maxima: x_max’ will have a different size (Assumed a single maximum, but there may be other maximums as well as higher or lower maximums.) The relative size goes to zero as $N \to \infty$ , $\frac{\exp (N ϕ (x^{'}))}{\exp (N ϕ (x))} = \exp (- N (ϕ (x) - ϕ (x^{'})))$ has a positive inner argument and an overall minus sign.

Write $ϕ (x) = \ln x - \frac{x}{N}$ . Then, $\int_{0}^{\infty} \exp (N ϕ (x)) d x = \int_{0}^{\infty} x^{N} \exp (- x) d x = Γ (N + 1)$ . $ϕ_{m} a x = ϕ^{'} (x) = \frac{1}{x} - \frac{1}{N}$ . Then the maximum is at $x = N$ . $ϕ (x_{m a x}) = \ln N - 1$ . $ϕ^{″} (x) = - \frac{1}{x^{2}} \to ϕ^{″} (x_{m a x}) = - \frac{1}{N^{2}}$ . So, $N! = \int_{0}^{\infty} x^{N} \exp (- x) \approx \exp (N ϕ (x_{m a x})) \int d x \exp (- \frac{N}{2} | ϕ^{″} (x_{m a x}) | (x - x_{m a x})^{2}) = \frac{N^{N}}{e^{N}} \sqrt{2 π N}$ .

Gamma Function

$\int d x x^{n} \exp (- x) = Γ (n + 1) = n!$ .

Partition Function

$Z = \sum_{α} \exp (- β E_{α})$ . $p_{α} = \frac{\exp (- E_{α} / k T)}{Z}$ .

$⟨ E ⟩ = \sum_{α} p_{α} E_{α} = - \frac{1}{Z} \partial_{β} Z = - \frac{\partial \ln Z}{\partial β}$ .

$\frac{\partial ⟨ E ⟩}{\partial T} = \frac{\partial ⟨ E ⟩}{\partial β} \frac{\partial β}{\partial T}$

C.f. $C_{V} = {(\frac{\partial U}{\partial T})}_{V, N}$

$C_{v} = f (⟨ E ⟩, ⟨ E^{2} ⟩) = γ (⟨ E^{2} ⟩ - ⟨ E ⟩^{2})$ .

Equations of State

Disorder

Entropy of Mixing

Consider a system with two parts of equal volume, $V$ . Total volume $2 V$ . $N$ total particles. Put the particles equally distributed in both regions, $N / 2$ . Color the left white and the right black. The entropy for the right or left atoms is then, $S_{W, B} = k_{B} \ln \frac{V^{N / 2}}{(\frac{N}{2})!}$ .

$Ω (E) = (\frac{V^{N}}{N!}) (\frac{(2 π m E)^{\frac{3 N}{2}}}{(\frac{3 N}{2})! h^{3 N}})$ = space * momentum.

$S_{u n m i x e d} = 2 S_{W, B} = 2 k_{B} \ln \frac{V^{N / 2}}{(N / 2)!}$ $S_{m i x e d} = 2 (k_{B} \ln \frac{(2 V)^{N / 2}}{(N / 2)!})$ . $Δ S_{m i x i n g} = S_{m i x e d} - S_{u n m i x e d} = 2 k_{B} \ln (\frac{(2 V)^{N / 2}}{V^{N / 2}}) = N k_{B} \ln 2$ .

Gibbs Paradox

If the particles were both black. $S_{u n m i x e d} = 2 S_{W, B} = 2 k_{B} \ln \frac{V^{N / 2}}{(N / 2)!}$ $S_{m i x e d} = k_{B} \ln \frac{(2 V)^{N}}{N!}$ . $Δ S_{m i x i n g} = S_{m i x e d} - S_{u n m i x e d} = k_{B} \ln (\frac{2^{N} (\frac{N}{2})!^{2}}{N!})$ . Using the Stirling approximation, $Δ S_{m i x i n g} / k_{B} = N \ln 2 + 2 (\frac{N}{2} \ln \frac{N}{2} - \frac{N}{2}) - (N \ln N - N) = N \ln N - N - N \ln 2 + N \ln 2 - (N \ln N - N) = 0$ .

Materials

Amorphous Solids

Glasses

The Solids are glasses if they have a glass transition.

If you heat up to a temperature $T$ then cool slowly, as you cool you phase transition between liquid and crystal solid at $T_{m e l t}$ . If you do it quickly to a temperature below $T_{glass}T_{glass}$). Viscosity changes abruptly. Examples: Covalent hotwork glasses: ${SiO}_{2}$ . Polymer glasses.

In order to redo a glass, you have to go back above $T_{m e l t}$ and recool to $T_{g}$ .

You get a unit of entropy (kB) per unit of material.

Theoretical glass models:

Spin-glasses. Consider a lattice of sites with spins $\pm 1$ . Say we have some random interaction $J s_{i} s_{j}$ . If $J$ is positive, then you need a even number of neighbors to get a non-frustrated glass. I.e. if you have a hexagonal lattice you get frustration. $- s l o w - > C r y s t a l - s l o w - > L i q u i d - f a s t - > G l a s s$ $S_{r e s} = S_{ℓ} (T_{ℓ}) - \int \frac{1}{T} \frac{d Q}{d t} d t = S_{ℓ} (T_{ℓ}) - \int_{0}^{T_{ℓ}} \frac{1}{T} \frac{d Q}{d T} d T \propto k_{B} \times # molecular units$ . Remark: $\frac{d Q}{d T}$ is the heat capacity.

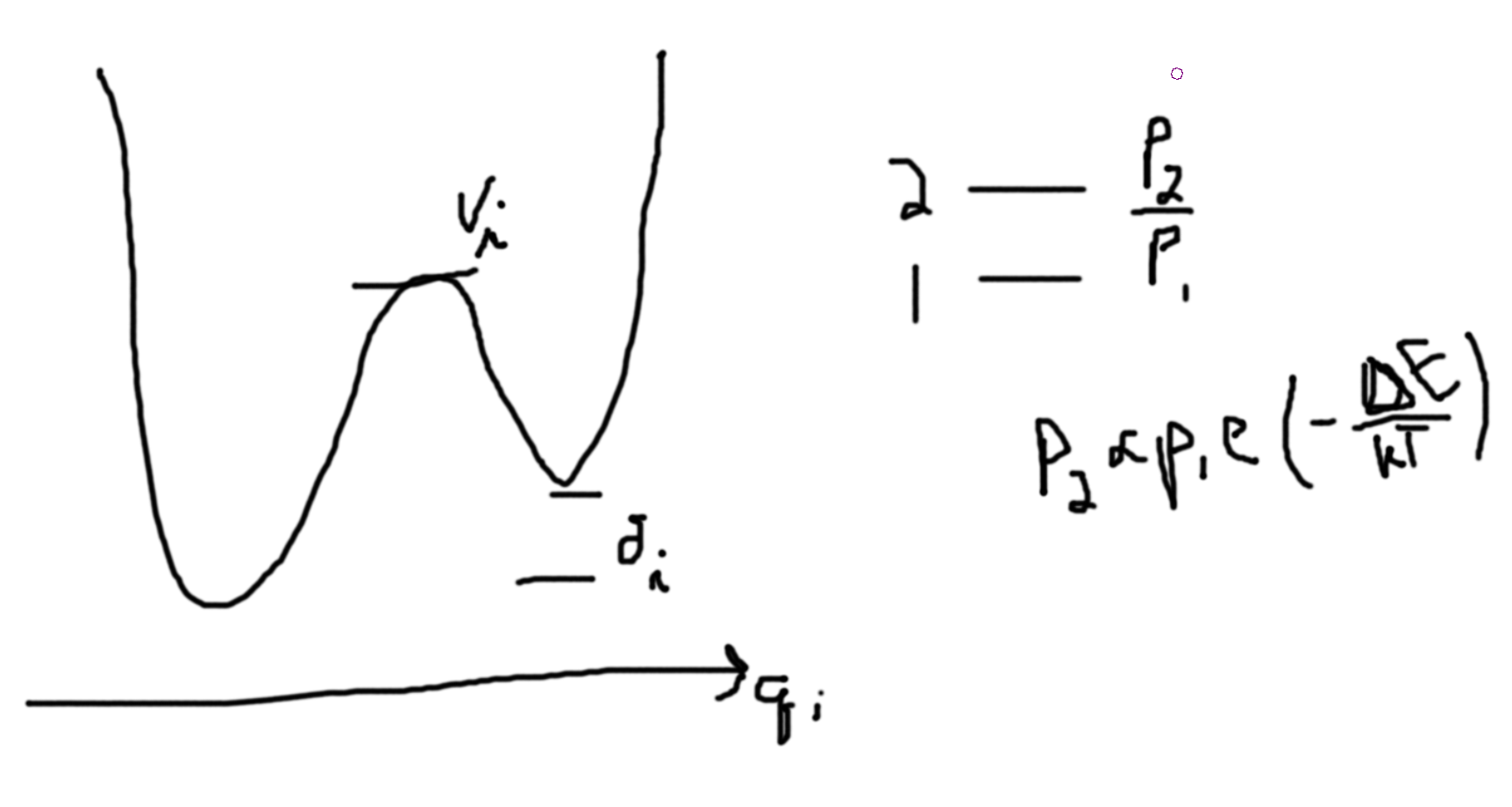
20230130110456-statistical_mechanics.org_20230227_111644.png

Assuming, $V_{i} ≫ δ_{i}$ . If kinetics is important minimal will be occupied roughly equally, $Δ S_{q_{i}} = k_{B} \ln 2$ . [then when you cool from the high temperature state (assuming $V_{i} ≫ δ_{i}$ ), you will find that some of the $2$ states will remain since they cannot traverse the barrier to get to the one state.]

The energy stored in the higher state by accident is $δ_{i}$ per $q_{i}$ , (50%). $Δ S_{q_{i}} \sim \frac{Δ Q_{i}}{T}$ . Note, we only have two temperatures, $T_{1} \sim \frac{V_{i}}{k_{B}}$ and $T_{2} \sim \frac{δ_{i}}{k_{B}} ≪ \frac{V_{i}}{k_{B}}$ . In our case, $T = T_{2}$ . We can call $T$ , $T_{f r e e z e}$ . So, $T_{f r e e z e} \sim \frac{δ_{i}}{k_{B}} ≪ \frac{V_{i}}{k_{B}} \sim \frac{δ_{i}}{\frac{δ_{i}}{k_{B}}} \sim k_{B}$ .

The time scale for this hopping is $τ \sim 10^{- 12}$ s.

Lenard-Jones potential - Annealing MC - 39 particles. Numerical does not give good results. Can only solve the system classically and then simulate the dynamics for reasonable results.

Information Theory

Initial Remarks

If you cannot get or use the information then the entropy does not change for a system. (The information to be put in the next process)

The information you can gain about the system. It is external to the system but is a state variable.

Lecture

$S_{d i s c r e t e} = - k_{B} ⟨ \ln p_{i} ⟩ = - k_{B} \sum_{i} p_{i} \ln p_{i} = - k_{B} \sum_{i} \frac{1}{W} \ln \frac{1}{W} = k_{B} \ln W = k_{B} \int_{E < H (P, Q) < E + δ E} \frac{d P d Q}{δ N} ρ (P, Q) \ln ρ (P, Q) = - k_{B} Tr (\hat{ρ} \ln \hat{ρ})$ with $ρ :=$ density matrix. Some texts call $⟨ \ln p ⟩$ the suprisal fuction, the ensemble average of ’suprise’.

Examples

Box: 3 balls: 1 red, 2 green.

For the first draw: $p (R) = \frac{1}{3}, p (G) = \frac{2}{3}$ .

If we put it back, we get independent draws. For the second draw (without putting back): $p (R_{2}) = p (R_{1}) p (R_{2} | R_{1}) + p (G_{1}) p (R_{2} | G_{1}) = 0 + \frac{2}{3} 1 = \frac{1}{3}$ , $p (G_{2}) = p (R_{1}) p (G_{2} | R_{1}) + p (G_{1}) p (G_{2} | G_{1}) = \frac{1}{3} (1) + \frac{2}{3} \frac{1}{2} = \frac{2}{3}$ .

For the third draw (without putting back): $p (R_{3}) = p (G_{1} G_{2}) p (R_{3} | G_{1} G_{2}) = p (G_{1}) p (G_{2} | G_{1}) p (R_{3} | G_{1} G_{2}) = \frac{2}{3} \frac{1}{2} = \frac{1}{3}$ . $p (G_{3}) = 1 - p (R_{3}) = \frac{2}{3}$ .

Measure of Suprise

What is information…

You won the Lottery! -> Huge suprise because it is highly unlikely. I.e. $p \to 0$ . So suprise $\to \infty$ .

You didn’t win the Lottery! -> ’Almost’ no suprise since it is highly likely. I.e. $p \to 1$ so suprise $\to 0$ .

Note, $- \ln p$ has this behavior.

Information

Notation: outcomes $A_{k}; k = 1, \dots, Ω; p_{k} = p (A_{k}); \sum_{k} p_{k} = 1; B_{ℓ}, ℓ = 1, \dots, M; q_{ℓ} = p (B_{ℓ}); \sum_{ℓ} q_{ℓ} = 1$ . For instance, if $A_{k}$ are the possible location for your keys and $B_{ℓ}$ are the locations that you last saw the keys.

Information is max if all the outcomes are equally likely. $S_{I} (\frac{1}{Ω}, \dots, \frac{1}{Ω}) \geq S_{I} (p_{1}, \dots, p_{Ω})$ with equality only if $p_{i} = \frac{1}{Ω} \forall i$ .
Information does not change if we add outcomes $A_{j}$ with $p_{j} = 0$ . $S_{I} (p_{1}, \dots, p_{Ω - 1}) = s_{I} (p_{1}, \dots, p_{Ω - 1}, 0)$ .
If we obtained (measure) partial information for a joint outcome $C = A \cdot B$ by measuring $B$ then $⟨ S_{I} (A | B_{ℓ}) ⟩_{B} = S_{I} (C) - S_{I} (B)$ where $⟨ S_{I} (A | B_{ℓ}) ⟩_{B} = \sum_{ℓ = 1}^{M} S_{I} (A | B_{ℓ}) q_{ℓ}$ . Note, $C_{k ℓ} = A_{k} \cdot B_{ℓ}, r_{k ℓ} = p (C_{k ℓ})$ . We use the average since we don’t know the answer a priori and so we must consider all of the possibilities. Once we have a specific $B_{ℓ}$ then that $q_{ℓ} = 1$ and the rest are zero, and so this still holds up.

$C_{k ℓ} = P (A_{k} | B_{ℓ}) = \frac{P (B_{ℓ} | A_{k}) P (A_{k})}{P (B_{ℓ})} = \frac{P (A_{k} \land B_{ℓ})}{p (B_{ℓ})} = \frac{P (A_{k} B_{ℓ})}{p (B_{ℓ})} = \frac{r_{k l}}{q_{ℓ}}$ .

$\sum_{k} c_{k ℓ} = \sum_{k} P (A_{k} | B_{ℓ}) = 1$ .

Before you talk to your roommate, $S_{I} (A \cdot B) = S_{I} (r_{11}, r_{12}, \dots, r_{1 M}, r_{21}, \dots, r_{Ω, M}) = S_{I} (c_{11} q_{1}, c_{12} q_{2}, \dots, c_{Ω M} q_{M})$ .

After you talked to your roomate, $S_{I} (A | B_{ℓ})$ . % = S(r_1ℓ,r_2ℓ,⋯,r_Ωℓ) Expected change in $S_{I}$ if you measure is given by (rule 3) $⟨ S_{I} (A | B_{ℓ}) ⟩_{B} = S_{I} (C) - S_{I} (B) = \sum_{ℓ = 1}^{m} S_{I} (A | B_{ℓ}) q_{ℓ}$ .

Proving 3. $S_{I} (C) = S_{I} (A B) = - k_{S} \sum_{k ℓ} r_{k ℓ} \ln r_{k ℓ} = - k_{S} \sum_{k ℓ} c_{k ℓ} q_{ℓ} \ln (c_{k ℓ} q_{ℓ}) = - k_{S} [\sum_{k ℓ} c_{k ℓ} q_{ℓ} \ln c_{k ℓ} + \sum_{k ℓ} c_{k ℓ} q_{ℓ} \ln q_{ℓ}] = \sum_{ℓ} q_{ℓ} (- k_{S} \sum_{k} c_{k ℓ} \ln c_{k ℓ}) - k_{S} \sum_{ℓ} [q_{ℓ} \ln (q_{ℓ}) \sum_{k} c_{k ℓ}] = \sum_{ℓ} q_{ℓ} (- k_{S} \sum_{k} c_{k ℓ} \ln c_{k ℓ}) - k_{S} \sum_{ℓ} [q_{ℓ} \ln (q_{ℓ})] = \sum_{ℓ} q_{ℓ} S_{I} (A | B) + S_{I} (B) = ⟨ S_{I} (A | B_{ℓ}) ⟩_{B} + S_{I} (B)$ .

Proving 2. $S_{I} = - k_{S} \sum_{k}^{Ω} p_{k} \ln p_{k} = - k_{S} \sum_{k}^{Ω - 1} p_{k} \ln p_{k} + lim_{p \to 0} p \ln p = S_{I}^{Ω - 1}$ .

Proving 1. $f (p) = - p \ln p$ . Thus, it is the information for 1 variable. $\frac{d f}{d p} = - \ln p - 1$ . $\frac{d^{2} f}{d p^{2}} = - \frac{1}{p} < 0$ for $p \in (0, 1)$ . Thus, $f (p)$ is concave.

For any points $a, b$ the weighted average $λ a + (1 - λ) b$ . Then,

\begin{matrix} (x) & (λ a + (1 - λ) b) \geq λ f (a) + (1 - λ) f (b) . \end{matrix}

Jensen inequality. $f (\frac{1}{Ω} \sum_{k} p_{k}) \geq \frac{1}{Ω} \sum_{k} f (p_{k})$ .

Consider $Ω = 2$ . In $(x)$ choose $λ = \frac{1}{2}$ , $a = p_{1}, b = p_{2}$ . Then, $f (\frac{p_{1} + p_{2}}{2}) \geq \frac{1}{2} (f (p_{1}) + f (p_{2}))$ .

For a general $Ω$ , choose $λ = \frac{Ω - 1}{Ω}$ , $a = \frac{1}{Ω - 1} \sum_{k} p_{k}$ and $b = p_{Ω}$ . Then by induction on $a$ and including $b$ with the $Ω = 2$ , we get the result we want. So, $f (\frac{1}{Ω} \sum_{k} p_{k}) = f (\frac{Ω - 1}{Ω} \sum_{k}^{Ω - 1} \frac{p_{k}}{Ω - 1} + \frac{1}{Ω} p_{Ω}) \geq \frac{Ω - 1}{Ω} f (\sum_{k}^{Ω - 1} \frac{p_{k}}{Ω - 1}) + \frac{1}{Ω} f (p_{Ω})$ Assuming the Jensen inequality is true, $f (\frac{1}{Ω} \sum_{k} p_{k}) = f (\frac{Ω - 1}{Ω} \sum_{k}^{Ω - 1} \frac{p_{k}}{Ω - 1} + \frac{1}{Ω} p_{Ω}) \geq \frac{Ω - 1}{Ω} f (\sum_{k}^{Ω - 1} \frac{p_{k}}{Ω - 1}) + \frac{1}{Ω} f (p_{Ω}) \geq \frac{1}{Ω} \sum_{k}^{Ω - 1} f (p_{k}) + \frac{1}{Ω} f (p_{Ω}) = \frac{1}{Ω} \sum_{k} f (p_{k})$ .

So, $S_{I} (p_{1}, \dots, p_{Ω}) = - k_{S} \sum_{k} p_{k} \ln p_{k} = k_{S} \sum_{k} f (p_{k}) = k_{S} Ω \frac{1}{Ω} \sum_{k} f (p_{k}) \leq k_{S} Ω f (\frac{1}{Ω} \sum_{k} p_{k}) = k_{S} Ω f (\frac{1}{Ω}) = - k_{S} Ω \frac{1}{Ω} \ln \frac{1}{Ω} = - k_{S} \ln \frac{1}{Ω} = S_{I} (\frac{1}{Ω}, \dots, \frac{1}{Ω})$ .

Conditional Probability

Definition: $p (B | A)$ is probability of event $B$ given event $A$ was observed.

Joint

$p (A \land B) = p (A B)$ .

Bayes Rule

$p (A B) = p (B | A) p (A) = p (A | B) p (B)$ .

Independent

For independent events, $p (B | A) = p (B)$ , $p (A | B) = p (A)$ . So, $p (A B) = p (A) p (B)$ .

Beyond the Microcanonical Ensemble

Information Theory Approach

Maximize entropy, minimize bias, principle.

Max: $S = - k_{B} \sum_{α} p_{α} \ln p_{α}$ subject to constraints using Lagrange parameters.

Constraints:

$\sum_{α} p_{α} = 1$
$⟨ E ⟩ = \sum_{α} p_{α} E_{α} \equiv E \equiv U$

If you do just (1), then you get $p_{α} = \frac{1}{N_{α}}$ .

If you do both (1+2), then $L = - k_{B} \sum_{α} p_{α} \ln p_{α} + λ_{1} k_{B} (1 - \sum_{α} p_{α}) + λ_{2} k_{B} (U - \sum_{α} p_{α} E_{α})$ .

$\frac{\partial L}{\partial p_{α}} = \dots = 0$

How does the temperature enter?

$λ_{2} = β = \frac{1}{k_{B} T}$ .

From the Microcanonical Ensemble

Recall we had the partitioned volume with sides at $S_{1}, E_{1}, ρ (E_{1})$ and $E - E_{1}$ with $ρ (S_{1}) = \frac{Ω_{2} (E - E_{1})}{Ω (E)}$ .

$ρ (E_{1}) = \frac{Ω_{1} (E_{1}) Ω_{2} (E - E_{1})}{Ω (E)}$ . Maximize $ρ (E_{1})$ leads to $\frac{1}{Ω_{1}} {(\frac{d Ω_{1}}{d E_{1}})}_{E_{1}^{*}} = \frac{1}{Ω_{2}} {(\frac{d Ω_{2}}{d E_{2}})}_{E - E_{1} *}$

Define $S$ : ${(\frac{d S_{1}}{d E_{1}})}_{E_{1}^{*}, V_{1}, N_{1}} = {(\frac{d S_{2}}{d E_{2}})}_{E - E_{1}^{*}, V_{2}, N_{2}}$

Define $T$ $\frac{1}{T_{1}} = \frac{1}{T_{2}}$ .

If we consider 1 as the system and 2 as the heat bath/ environment, So, $ρ (S) = \frac{Ω_{2} (E - E_{S})}{Ω (E)} = \frac{1}{Ω (E)} \exp (\frac{S_{2} (E - E_{S})}{k_{B}})$ .

Comparing two states, $S_{A}, E_{A}$ and $S_{B}, E_{B}$ . Assume $E_{B} > E_{A}$ , but this is not required.

$\frac{ρ (S_{B})}{ρ (S_{A})} = \frac{Ω_{2} (E - E_{B})}{Ω_{2} (E - E_{A})} = \exp (\frac{S_{2} (E - E_{B}) - S_{2} (E - E_{A})}{k_{B}})$

Note, $S_{2} (E - B_{B}) - S_{2} (E - E_{A}) \approx (E_{A} - E_{B}) (\frac{\partial S}{\partial E})$

This comes from $Δ S_{2} = \frac{Δ E_{2}}{T}$ . So, $Δ E_{s y s} = Δ E_{1} = E_{B} - E_{A}$ . So, $Δ E_{e n v} = - Δ E_{s y s} = E_{A} - E_{B}$ .

Then, probability in being in a particular state is $ρ (S) \propto \exp (- \frac{E_{S}}{k_{B} T}) = \exp (- β E_{S})$ .

Normalization: $s u m_{α} ρ (S_{α}) = 1 \Rightarrow ρ (S) = \frac{\exp (- β E_{S})}{\sum_{α} \exp (- β E_{α})} = \frac{1}{Z} \exp (- β E_{S})$ .

$Z = \sum_{α} \exp (- β E_{α}) = \int \frac{d P_{1} Q_{1}}{h^{3 N_{1}}} \exp (- \frac{H_{1} (P_{1}, Q_{1})}{k T}) = \int d E_{1} Ω_{1} (E_{1}) \exp (- \frac{E_{1}}{k T})$ .

Internal energy: $⟨ E ⟩ = \sum_{α} p_{α} E_{α} = \frac{1}{Z} \sum_{α} E_{α} \exp (- β E_{α}) = - \frac{\partial \ln Z}{\partial B}$ .

Heat capacity at a constant volume: $c_{V} = {(\frac{\partial U}{\partial T})}_{V, N} = (\frac{\partial ⟨ E ⟩}{\partial T}) = \frac{\partial ⟨ E ⟩}{\partial β} \frac{\partial β}{\partial T} = - \frac{1}{k_{B} T^{2}} \frac{\partial ⟨ E ⟩}{\partial β} = \frac{1}{k_{B} T^{2}} \frac{\partial^{2} \ln Z}{\partial β^{2}}$ . $c_{V} = T {(\frac{\partial S}{\partial T})}_{V}$ .

$\frac{\partial ⟨ E ⟩}{\partial β} = - \frac{\partial}{\partial β} \frac{\sum_{α} E_{α} \exp (- β E_{α})}{\sum_{α} \exp (- β E_{α})} = \frac{1}{Z^{2}} (\sum_{α} (- E_{α}) \exp (- β E_{α})) (\sum_{α} E_{α} \exp (- β E_{α})) + \frac{1}{Z} \sum_{α} E_{α}^{2} \exp (- β E_{α}) = - ⟨ E ⟩^{2} + ⟨ E^{2} ⟩ = ⟨ (E - ⟨ E ⟩)^{2} ⟩ = ⟨ E^{2} - 2 E ⟨ E ⟩ + ⟨ E ⟩^{2} ⟩ = ⟨ E^{2} ⟩ - ⟨ E ⟩^{2}$ .

The total heat capacity is then $C_{V} = N {\tilde{c}}_{V} = \frac{1}{k_{B} T^{2}} (⟨ E^{2} ⟩ - ⟨ E ⟩^{2}) = \frac{σ_{E}^{2}}{k_{B} T^{2}}$ .

The energy fluctuations per particle is $\frac{σ_{E}}{N} = \frac{\sqrt{⟨ E^{2} ⟩ - ⟨ E ⟩^{2}}}{N} = \frac{\sqrt{N {\tilde{c}}_{V} k_{B} T^{2}}}{N} = \frac{\sqrt{k_{B} T} \sqrt{{\tilde{c}}_{V} T}}{\sqrt{N}}$ . The second square root is related to the amount of heat required to rais individual particle temperatures.

So, for large systems the energy fluctuations per particle remain small. So you can analyze the system cannonically or microcannonically.

$S = - k_{B} \sum_{α} p_{α} \ln p_{α} = - k_{B} \sum_{α} \frac{\exp (- β E_{α})}{Z} \ln (\frac{\exp (- β E_{α})}{Z}) = - k_{B} \frac{1}{Z} \sum_{α} (\exp (- β E_{α}) \ln (- β E_{α} - \ln Z)) = k_{B} β ⟨ E ⟩ + k_{B} \ln Z \sum_{α} \frac{\exp (- β E_{α})}{Z} = k_{B} \ln Z + \frac{⟨ E ⟩}{T}$ . So, $- k_{B} T \ln Z = ⟨ E ⟩ - T S = U - T S = F$ .

Thus, we get the Helmholtz free energy from the partition function.

Equivalently, $Z = \exp (- β F)$ .

So, connecting a system to a heat bath is the most basic assumption we need to derive our thermodynamic quantities we are familiar with.

Exercise

We have, $Z = \exp (- β E) = \exp (- β H)$ . Consider a conjugate pair, $X, y$ (i.e. y is a generalized force and X is a generalized displacement), then $X = \frac{\partial X}{\partial y}$ . We then get $Z = \exp (- β (H - X y))$ . So, $E = E (X)$ for internal energy.

Quantum Statistical Mechanics

$N (μ) = \int_{0}^{\infty} d ϵ g (ϵ) n (μ, T) d ϵ$ .

For 3D: $g (ϵ) = (4 π p^{2}) (\frac{d | \vec{p} |}{d ϵ}) {(\frac{L}{(2 π ℏ)})}^{3}$ . For 2D: $g (ϵ) = (2 π p) (\frac{d | \vec{p} |}{d ϵ}) {(\frac{L}{(2 π ℏ)})}^{2}$ . For 1D: $g (ϵ) = (2) (\frac{d | \vec{p} |}{d ϵ}) {(\frac{L}{(2 π ℏ)})}^{1}$ .

Density Matrices

Gibbs Phase Rules

Thermal Equilibrium

Particles in thermal equilibrium follow a boltzman distribution.

Ising Model

Symmetries and Order Parameters

Correlations

Suceptibility

Nucleation

We are reaching for droplet formation from gas to liquid abrupt phase transition.

$Δ G = G_{g a s} - G_{l i q u i d}$ Dividing across by $N$ , $Δ μ = \frac{Δ G}{N} = \frac{G_{g a s} - G_{l i q u i d}}{N}$ .

$Δ G \approx \frac{\partial (G_{g} - G_{ℓ})}{\partial T} Δ T = (S_{ℓ} - S_{g}) Δ T$ So, $Δ μ \approx \frac{(S_{ℓ} - S_{g}) Δ T}{N}$ . And, $Δ S_{L - G} = \frac{Q}{T_{v}} = \frac{L \cdot N}{T_{v}}$ . So, $Δ μ = \frac{L Δ T}{T_{v}}$ .

Consider a droplet of volume $V_{D}$ . Then, $Δ G \propto V_{D}$ which lowers the free energy. The surface costs energy: $\propto σ A_{D}$ where $σ$ is the surface tension and raises the free energy.

$Δ G = 4 π R^{2} σ - \frac{4}{3} π R^{3} \frac{N Δ μ}{V} = 4 π R^{2} σ - \frac{4}{3} π R^{3} n Δ μ$ . Then, we get some critical radius, $R_{c}$ between these two competing free energies. $R_{c} = \frac{2 σ}{n Δ μ} = \frac{2 σ T_{v}}{n L Δ T}$ gives the critical radius of the droplet. Hence, for lower barriers (lower latent heat) the critical radius increases. The barrier, $B = \frac{16 π σ^{3} T_{v}^{2}}{3 n^{2} L^{2} (Δ T)^{2}}$ .

Conserved order parameter: (mass) requires conservation of quantities. Non-conserved order parameter: (magnetism).

Introduction to Phenomonological Scaling

$α$ : $C_{β} \propto {| \frac{T - T_{c}}{T} |}^{- α}$ where $T \to T_{c}$ and $B = 0$ .
$β$ : $m \propto (T_{c} - T)^{β}$ where $T \to T_{c}$ , $T > T_{c}$ , and $B = 0$
$γ$ : $χ \propto | T_{c} - T |^{- γ}$ where $T \to T_{c}$ and $B = 0$
$δ$ : $m \propto B^{1 / δ}$ where $T = T_{c}$ and $B = 0$
$η$ : $C_{c}^{(2)} (r) p r o p t o \frac{1}{r^{d - 2 + η}}$ where $T = T_{c}$ and $B = 0$
$ν$ : $C_{c}^{(2)} (r) \propto \exp (- r / ξ)$ and $ξ \propto | T - T_{c} |^{- ν}$ for $B = 0$ and $T$ near $T_{c}$

Widom Scaling Hypothesis. The free energy, $f (T, B) = t^{1 / y} ψ (\frac{B}{t^{x / y}})$ where $t = \frac{| T - T_{c} |}{T_{c}}$ . So, $z = \frac{B}{t^{x / y}} \to t^{x / y} = \frac{1}{z} \frac{B}{z} \Leftrightarrow t^{1 / y} = \frac{B^{1 / x}}{z^{1 / x}}$ . So, $f (T, B) = B^{1 / x} z^{- 1 / x} Ψ (z) = B^{1 / x} \tilde{ψ} (\frac{B}{t^{x / y}})$ . Then, $m_{B = 0} = - {(\frac{\partial f}{\partial B})}_{T} = - t^{(1 - x) / y} ψ^{'} (0)$ and $β = \frac{1 - x}{y}$ . From this, we can calculate the first 4, which come in combinations of $x$ and $y$ . For $χ$ , $γ = \frac{2 x - 1}{y}$ . For $C_{B}$ , $α = 2 - \frac{1}{y}$ . Also, $δ = \frac{1}{x} - 1$ .

Hausdorf Scaling Hypothesis, $C_{c}^{(2)} (r, t) = \frac{ψ (r t^{\frac{2 - α}{d}})}{r^{d - 2 + η}}$ . So, $γ d = α - 2$ . From all of these, we see that 5-6 only depend on 2 parameters needed.