Gibbs Phase Rules

$n_{w}$ : Number of ways to do work $n_{c}$ : Number of chemical +1: Heating/ cooling $N = n_{w} + n_{c} + 1$ is the number of intensive parameters.

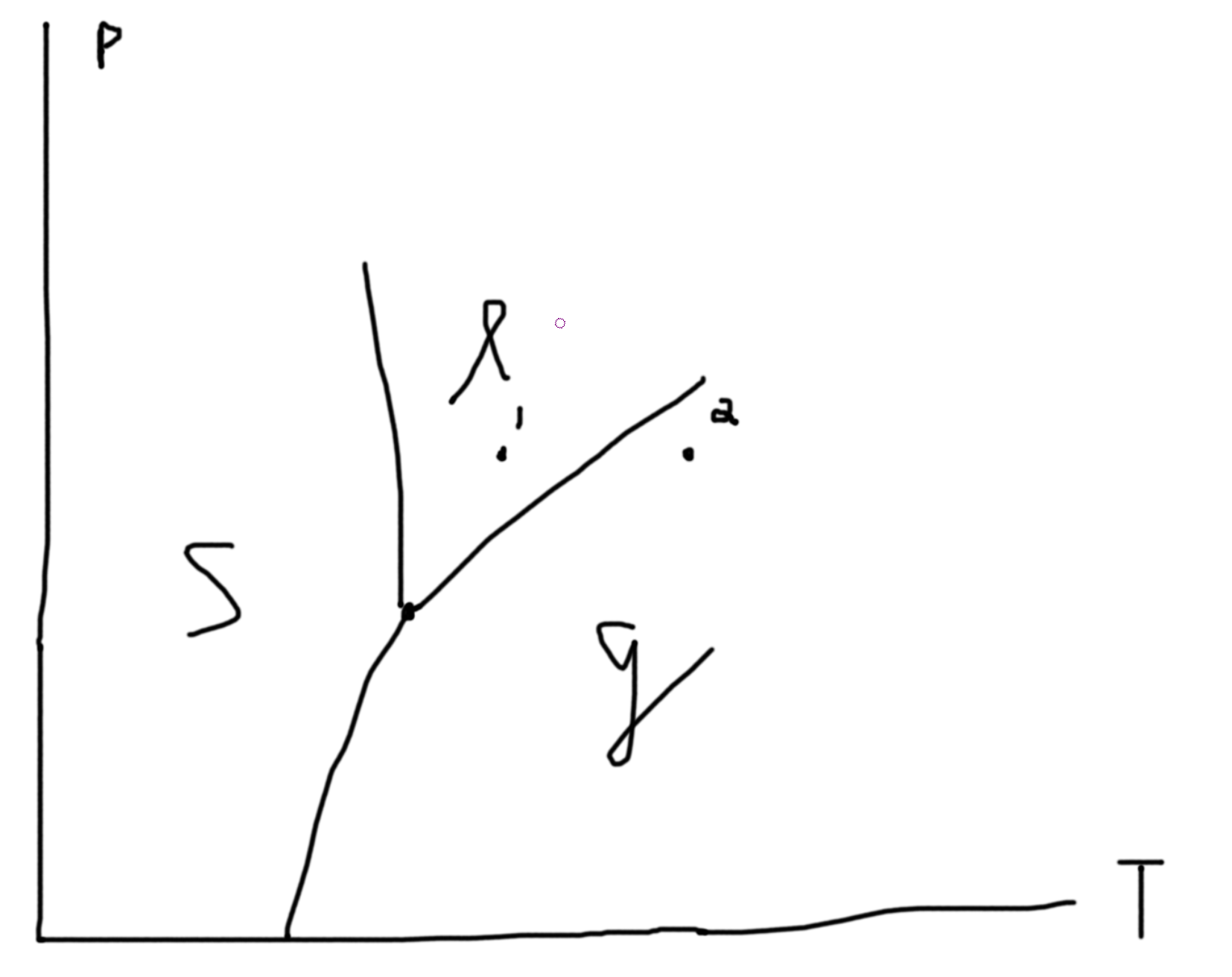
Constraints: If 2 phases coexist $μ_{ℓ} = μ_{g}$ is one constraint. If 3 phases coexist $μ_{ℓ} = μ_{g}$ and $μ_{ℓ} = μ_{s}$ gives 2 constraints. So, let $p$ be the number of constraints. Then the degrees of freedom in our system is $f = n_{w} + n_{c} + 1 - p$ . Suppose we have 1 species $(n_{c} = 1)$ and 1 way of doing work (mechanical/ pressure for example) so $f = 3 - p$ . If we have 1 phase, $p = 1$ so $f = 2$ and so $p (T)$ is an area. If we have 2 phases, $p = 2$ so $f = 1$ and so $p (T)$ is a line. If we have 3 phases, $p = 3$ so $f = 1$ and so $p (T)$ is a point (triple point).

Say we fix $N$ , then we can plot $P$ versus $V / N$ .

20230130110456-statistical_mechanics.org_20230414_111217.png

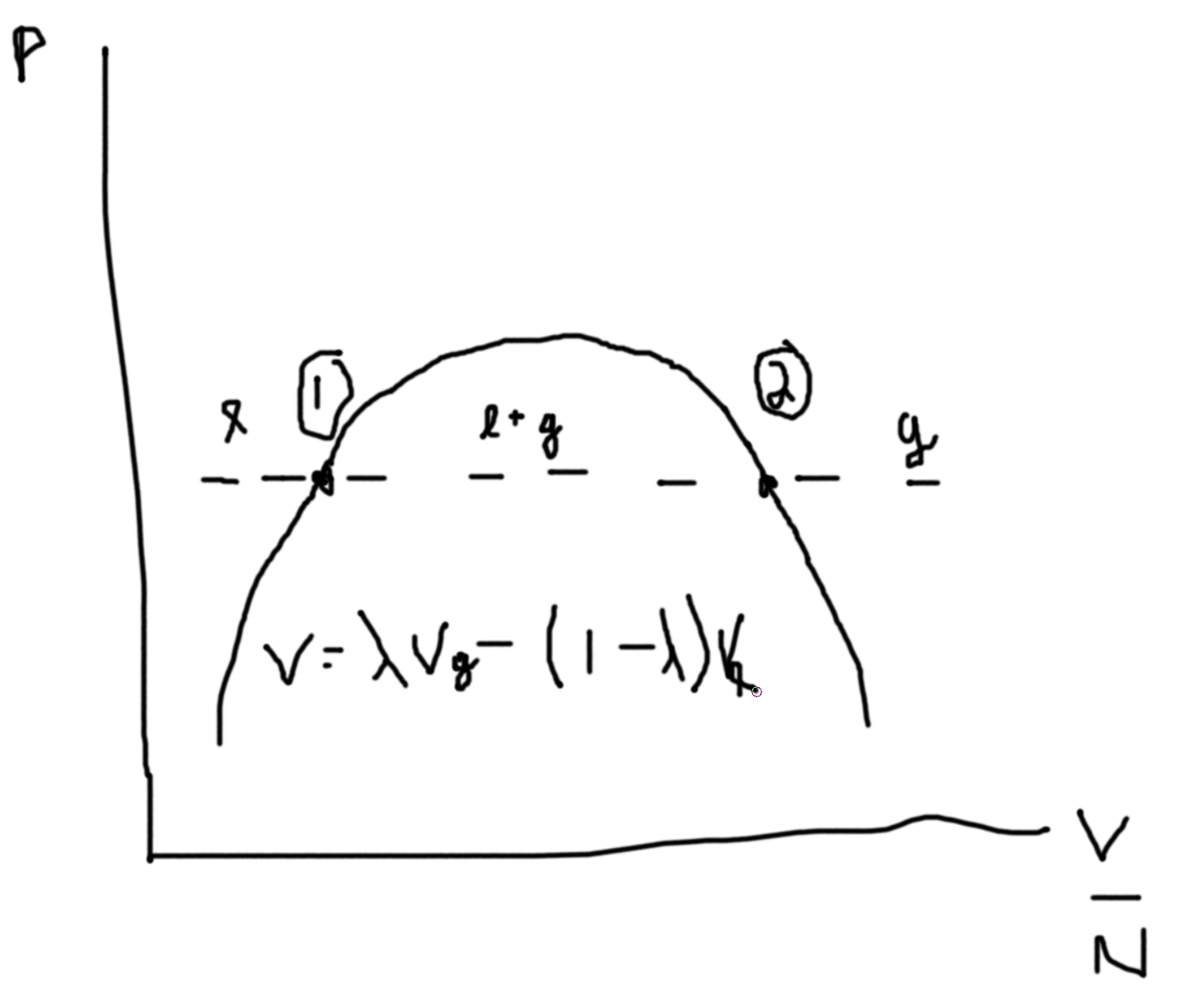
20230130110456-statistical_mechanics.org_20230414_111310.png

20230130110456-statistical_mechanics.org_20230414_111850.png

C.f. Suppose we have an alloy: 20230130110456-statistical_mechanics.org_20230414_111829.png

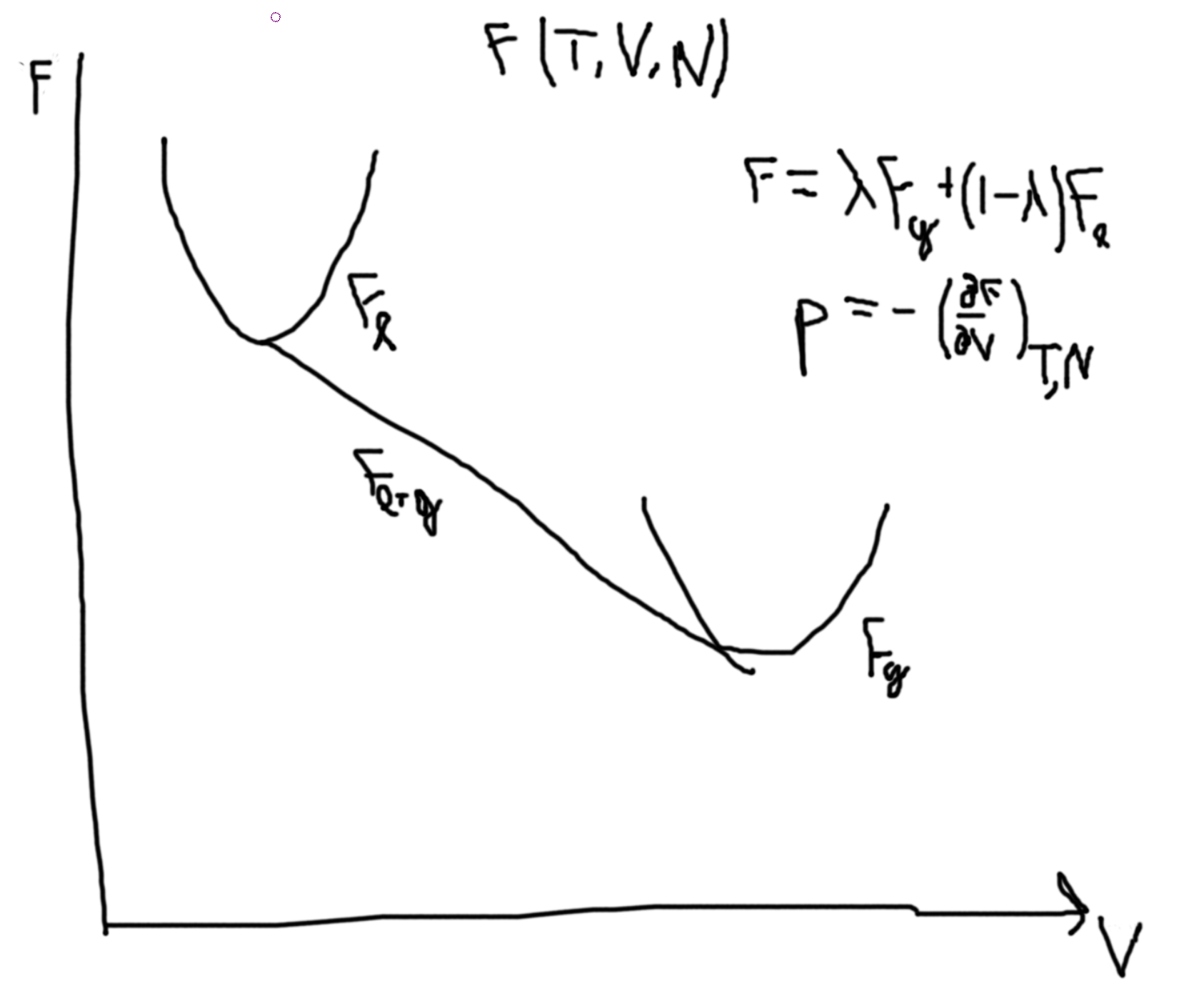
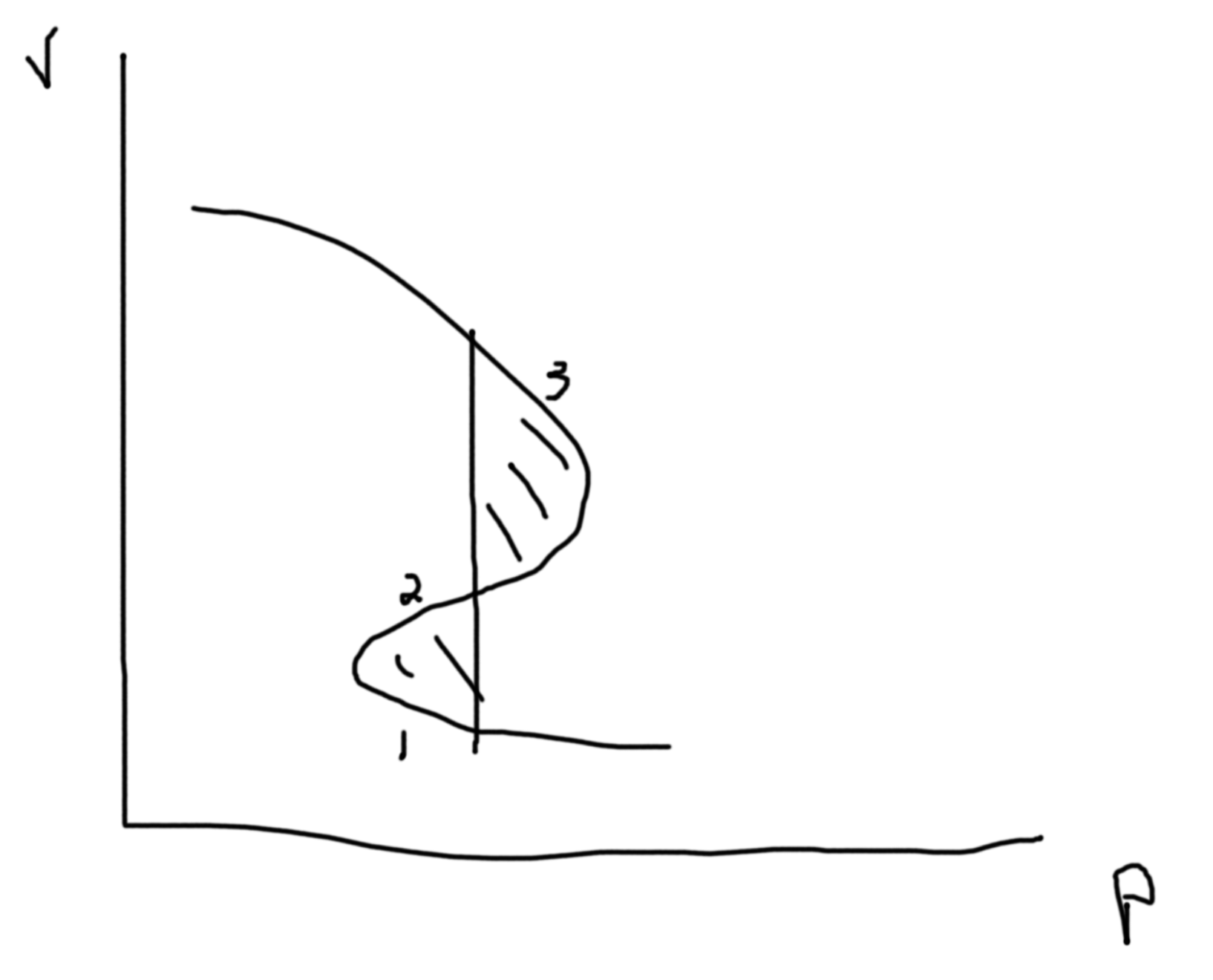
Suppose that we have a constant temperature $\to G (T, p, N)$ .

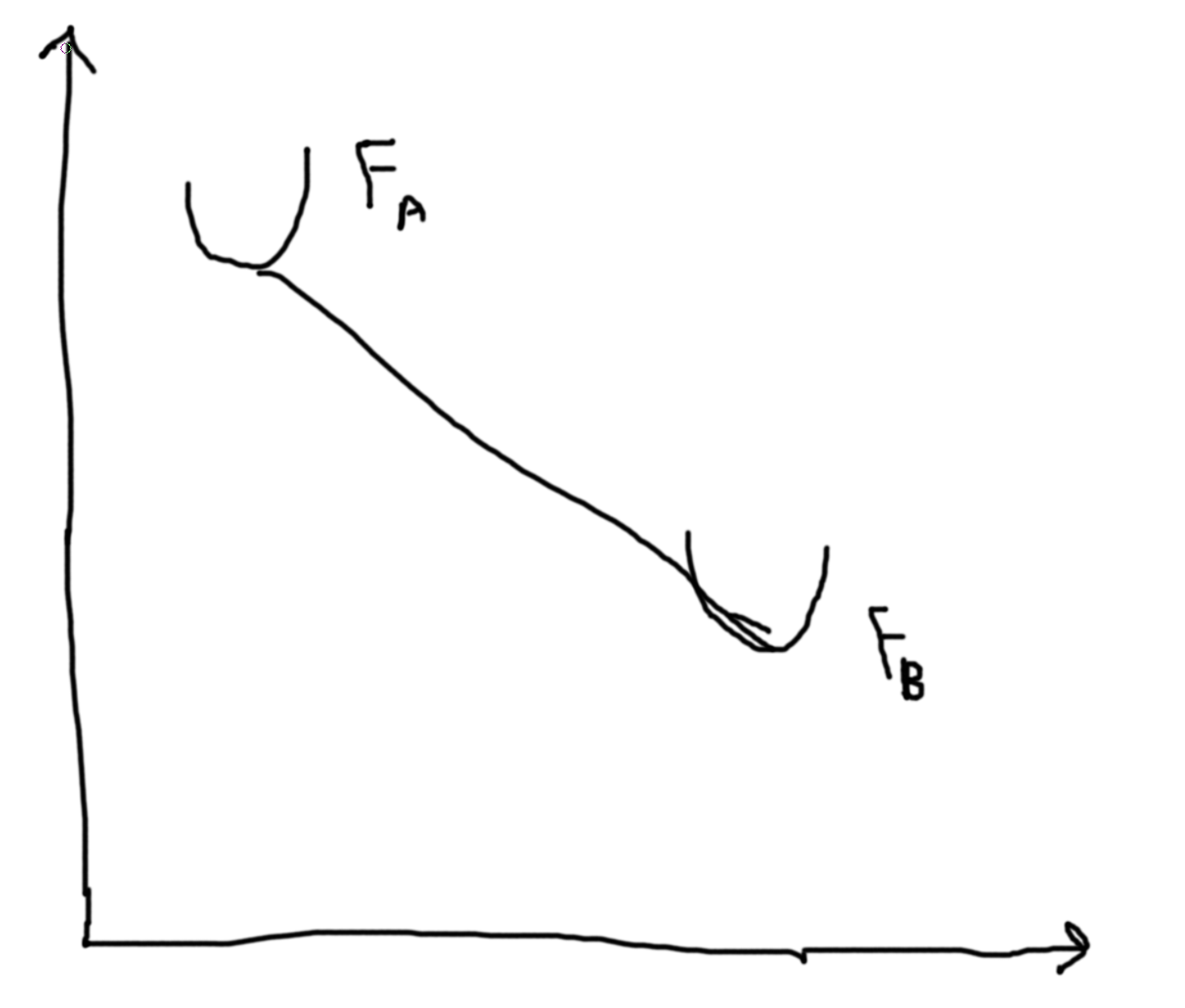
Then the Gibbs free energy of a liquid, we have a similar picture as $F$ with $T$ and $N$ . So, plotting $G (p, T, N)$ versus temperature, we get two lines for liquids and gas that intersect at $T_{T}$ . The liquid line has a more gradual slope and a lower intercept. In the region before the $T_{T}$ the gas line is called a supercooled gas and in the region after the liquid line (now above the gas line) is called a superheadted liquid.

So, $G (T, p, N) = μ N \Rightarrow μ = \frac{G}{N}$ . I.e. the chemical potential of liquid is less than that of a gas. $S = - {(\frac{\partial G}{\partial T})}_{P, N}$ . $Δ S_{ℓ - g} = \frac{Q}{T} = \frac{L N}{T}$ where $L$ is the latent heat per particle. Hence, $L = \frac{Δ S \cdot T}{N}$ . IMPORTANT To compute the latent heat you need to compute the entropy change. $Δ S =$ change in the slopes at the transition temperature.

Van der Waals Equation of State

$(p + a \frac{N^{2}}{V^{2}}) (V - N b) = N k T$ $a$ measures the attractive forces and $b$ measures the volume taken up by each particle.

Recall analysis from previous homeworks. $p (V) \propto V^{γ}$ .

Stability conditions. For each conjugate pair you have (x, f) then ${(\frac{\partial x}{\partial f})}_{*} \geq 0$ . Except, $α = \frac{1}{V} \frac{\partial V}{\partial T} \geq or \leq 0$ . Compressibility gives condition for unstable states.

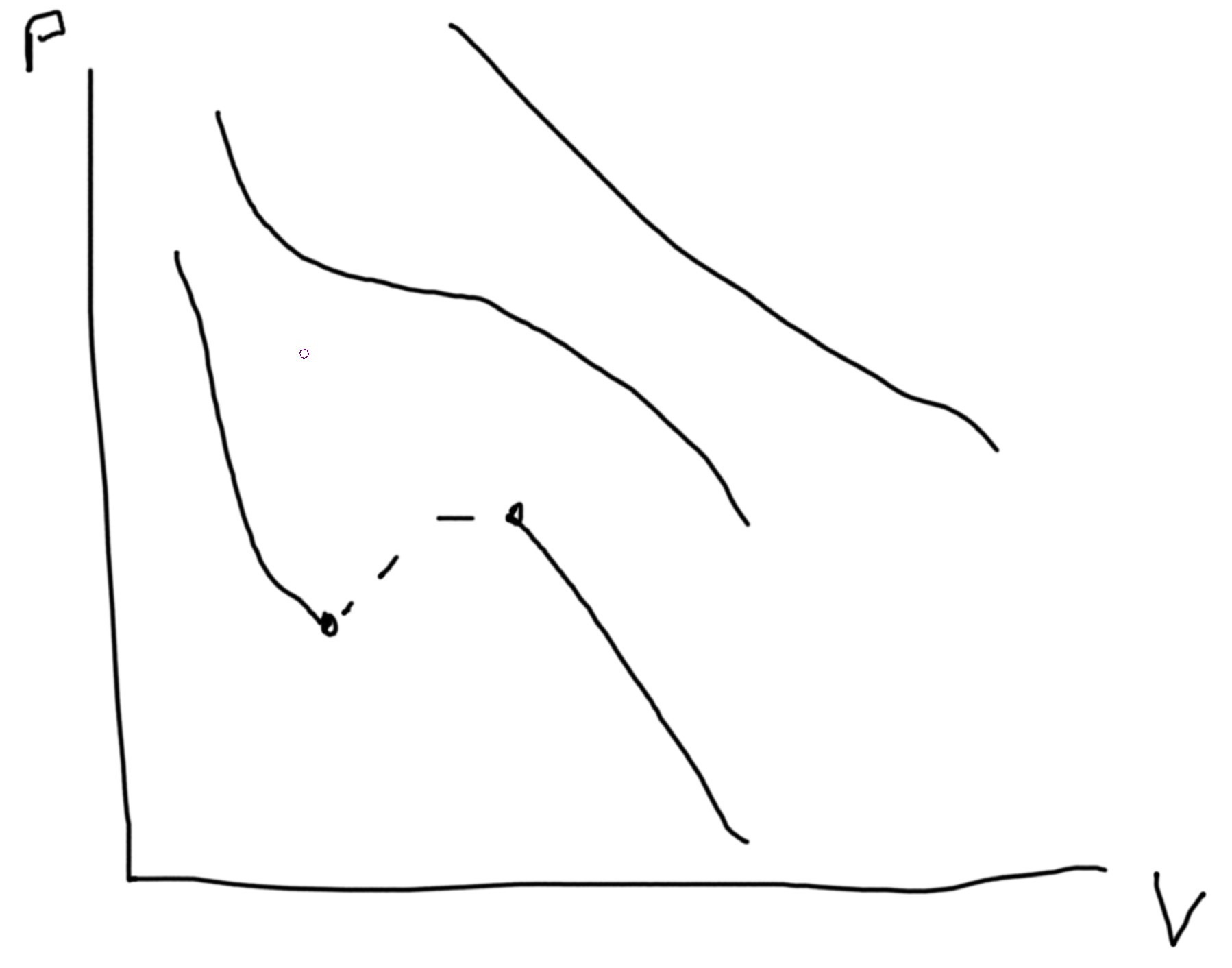Between the two points we can draw a line at constant $P$ such that area above equals area below. This denotes area of equal coexistence and so $μ_{ℓ} = μ_{g}$ . The dotted lines are unphysical regions. 20230130110456-statistical_mechanics.org_20230414_113729.png From $p \leftrightarrow G$ , $d G = - S d T + V d p + μ d N$ . So $Δ G_{ℓ - g} = \int_{ℓ}^{g} d G = \int_{p_{ℓ}}^{p_{g}} V (p)$ .

For a Reaction

$3 H_{2} + N_{2} ⇌ 2 N H_{3}$ . In this setup, these could all be in a gaseous state. Assume this is the case. So $[H_{2}]^{3} [N_{2}] k_{R} (T) = Γ_{R} (T, p)$ and $Γ_{L} (T) = k_{L} (T) [N H_{3}]^{2}$ . Then, $\frac{[N H_{3}]^{2}}{[H_{2}]^{3} [N_{2}]} = k_{e q} (T)$ . This is the Law of mass action. Finding $k_{e q} (T)$ we use the knowledge we are in gas phase and chemical potentials are equal.

Treat each constituent as an ideal gas. $Z \to F \to μ (T)$ . $Δ F = (\frac{\partial F}{\partial N_{H_{2}}}) Δ N_{H_{2}} + (\frac{\partial F}{\partial N_{N_{2}}}) Δ N_{N_{2}} + (\frac{\partial F}{\partial N_{N H_{3}}}) Δ N_{N H_{3}}$

Considering the rightwards direction: $Δ F_{R} = - 3 μ_{H_{2}} - μ_{N_{2}} + 2 μ_{N H_{3}}$ . $Δ F_{L} = - Δ F_{R}$ .

$F (T, V, N) = N k T (\ln \frac{N}{V} λ^{3} - 1) + N F_{0}$ where the last term arises from the internal degrees of freedom of each of the $N$ particles. So, $μ (T, V, N) = {(\frac{\partial F}{\partial N})}_{T, V} = k T (\ln \frac{N}{V} λ^{3} - 1) + N k T \frac{1}{N} + F_{0} = k T \ln \frac{N}{V} + k T \ln λ^{3} + F_{0} = k T \ln \frac{N}{V} + C (T) + F_{0}$ . Inserting this in $- 3 μ_{H_{2}} - μ_{N_{2}} + 2 μ_{N H_{3}} = 0$ , we get $- 3 \ln [H_{2}] - \ln [N_{2}] + 2 \ln [N H_{3}] = 2 C_{H_{2}} + C_{N_{2}} - 2 C_{N H_{3}} + 3 F_{0, H_{2}} + F_{0, N_{2}} - 2 F_{0, N H_{3}} = - Δ F_{n e t}$ . Then, $\frac{[N H_{3}]^{2}}{[H_{2}]^{3} [N_{2}]} = k_{e q} (T) = k_{0} \exp (- \frac{Δ F_{n e t}}{k T})$ . Recall, $Δ F = Δ E - T Δ S \approx Δ E_{n e t}$ for solids and chemistry. Then, $k_{0} = \frac{λ_{H_{2}}^{9} λ_{N_{2}}^{3}}{λ_{N H_{3}}^{6}} = \frac{h^{6} m_{N H_{3}}^{3}}{8 π (k_{B} T)^{3} m_{H_{2}}^{9 / 2} m_{N_{2}}^{3 / 2}} \propto T^{- 3}$ .

Aside: C.f. with hydrogen atom, $\frac{[p] [e]}{[H]} = k (T)$ with $n \cdot p = k (T)$ .

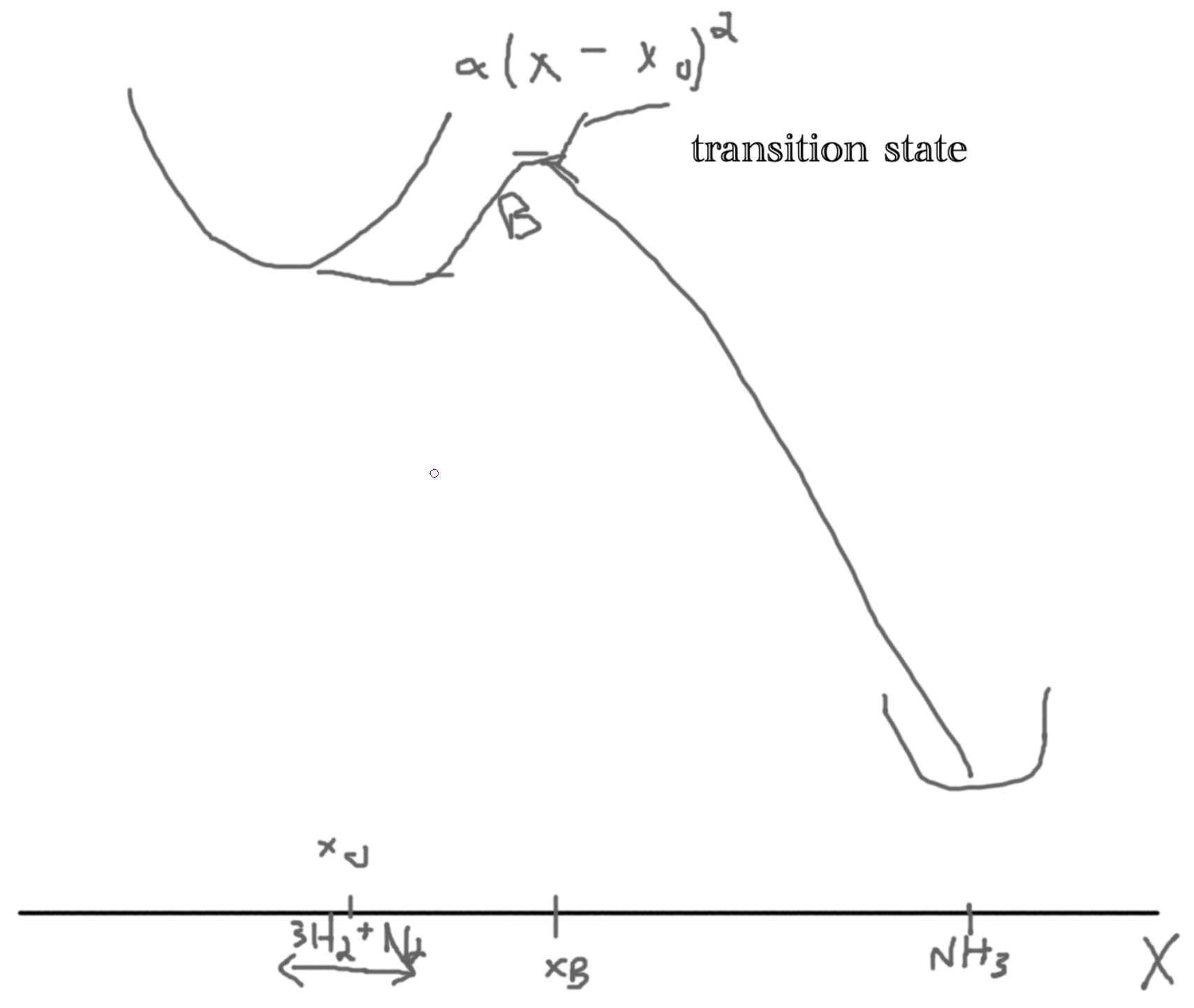Consider the one way reaction consisting of 5 particles, $3 H_{2} + N_{2} \to N H_{3}$ . If we have $M$ particles then we get a 3M dimensional space. Then we want to minimize energy in our 3M-1 dimensional space. Let $X$ be the reaction coordinate. Let the y-axis be the energy. 20230130110456-statistical_mechanics.org_20230419_112240.png We argue that the rate is proportional to the Boltzman factor, $γ \propto \exp (- \frac{B}{k T})$ , problem 6.11. The assumptions are: no recrossing, reactions are in local equilibrium (in ’well’), equal distribution determines the number of particles crossing the well. Let the probability distribution of the particles $ρ (x)$ . Then the probability distribution at the bottom of the well is $ρ (x_{0})$ and at the barrier $ρ (x_{b})$ such that $\frac{ρ (x_{b})}{ρ (x_{0})} = \frac{\exp (- U (x_{B}) / k T)}{\exp (- U (x)) / k T} = \exp (- B / k T)$ . Since $B ≫ k T$ , most particles are near $x_{0}$ . Then, $U (x) = \frac{1}{2} M ω^{2} (x - x_{0})^{2}$ . So, $ρ (x) = \sqrt{\frac{m ω^{2}}{2 π k T}} \exp (- \frac{m ω^{2}}{2 k T} (x - x_{0})^{2})$ And so, $ρ (x_{0}) = \sqrt{\frac{m ω^{2}}{2 π k T}}$ .

If the particle is $Δ x$ away from the top of the barrier with velocity $v$ then $Δ x = v Δ t$ gives the rate $Γ_{V} = ρ (x_{B}) v \frac{Δ t}{Δ t} = ρ (x_{b}) v$ . So, for all positive velocities, $Γ = \int_{0}^{\infty} d v Γ_{v} ρ (v)$ . Then, we are in equilibrium our velocities are normal distributed velocities, $ρ (v) \propto \exp (- E_{k i n} / k T) = \exp (- \frac{M v^{2}}{k T})$ so $ρ (v) = \sqrt{\frac{M}{2 π k T}} \exp (- \frac{M v^{2}}{2 k T})$ . Thus, $Γ = ρ (x_{B}) \int_{0}^{\infty} v ρ (v) d v = \frac{ω}{2 π} \exp (- \frac{B}{k T})$ . Using multidimensional transition rate: $Γ = \frac{\prod_{i} ω_{i}}{2 π \prod_{j} ω_{j, B}} \exp (- \frac{B}{k T})$ . Where $ω_{j, B}$ denotes the saddle points.

If $ω$ is large we get a steep well.

Thus, in general it is difficult to analyze kinetic behaviors from equilibrium treatments.