Symmetries and Order Parameters

Start out with a system (with properties and dynamics) described by its Hamiltonian $H$ . $H$ is invariant under some group $G$ , which give the symmetries of $H$ .

A system can have states with symmetries lower than the full group of the Hamiltonian, i.e. the state is invariant under some subgroup $G$ . We call those symmetry breaking.

Our state is described by thermodynamic (ensemble) averages of operators $ϕ_{α}$ , the ensemble average is then $⟨ ϕ_{α} ⟩, ⟨ ϕ (x) ⟩$ which is not invariant under the full group $G$ .

These averages (⟨Φ⟩) are called order parameters. $⟨ ϕ ⟩$ is a global order parameter and $⟨ ϕ (x) ⟩$ is a local order parameter.

We can choose that the global order parameter is zero for high symmetry (always the full group, hence high T).

Symmetries

Discrete symmetries $Z_{2}$ , group 2 integers. Ex. Ising symmetries, uniaxial (anti-)ferromagnetic system. FM: $(⟨ m_{z} ⟩)$ . AFM: $⟨ m_{z, A} - m_{z, B} ⟩$ . Ex: Rb $_{2}$ NiF $_{4}$ , K $_{2}$ MnF $_{4}$ . Order-disorder: Binary-order $⟨ n_{A} - n_{B} ⟩$ $[β - brass]$ . Liquid-gas: $⟨ n_{L} - n_{g} ⟩$ .

Dispacive: (Ferroelectric) perouskite $⟨ n_{z} ⟩$ BaLiO $_{3}$ .

20230130110456-statistical_mechanics.org_20230508_112229.png

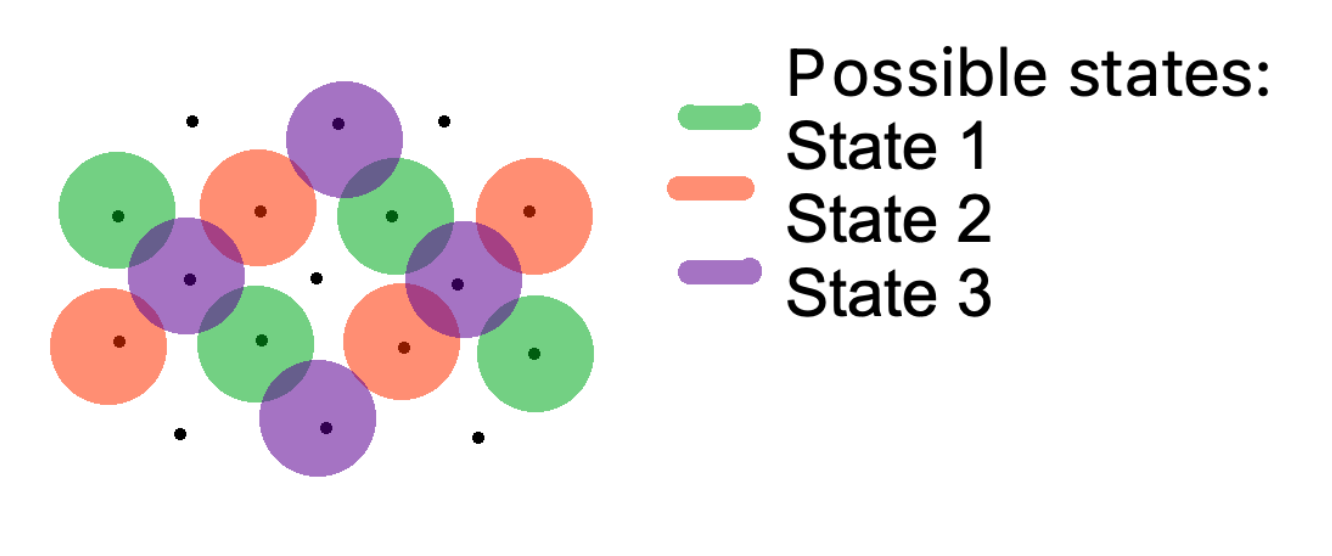
$Z_{3}$ group 3 integers. Graphene/ graphite surface (Krypton occupations on graphene lattice).

20230130110456-statistical_mechanics.org_20230508_112630.png

$Z_{N}$ group $N$ integers.

Continuous Symmetries:

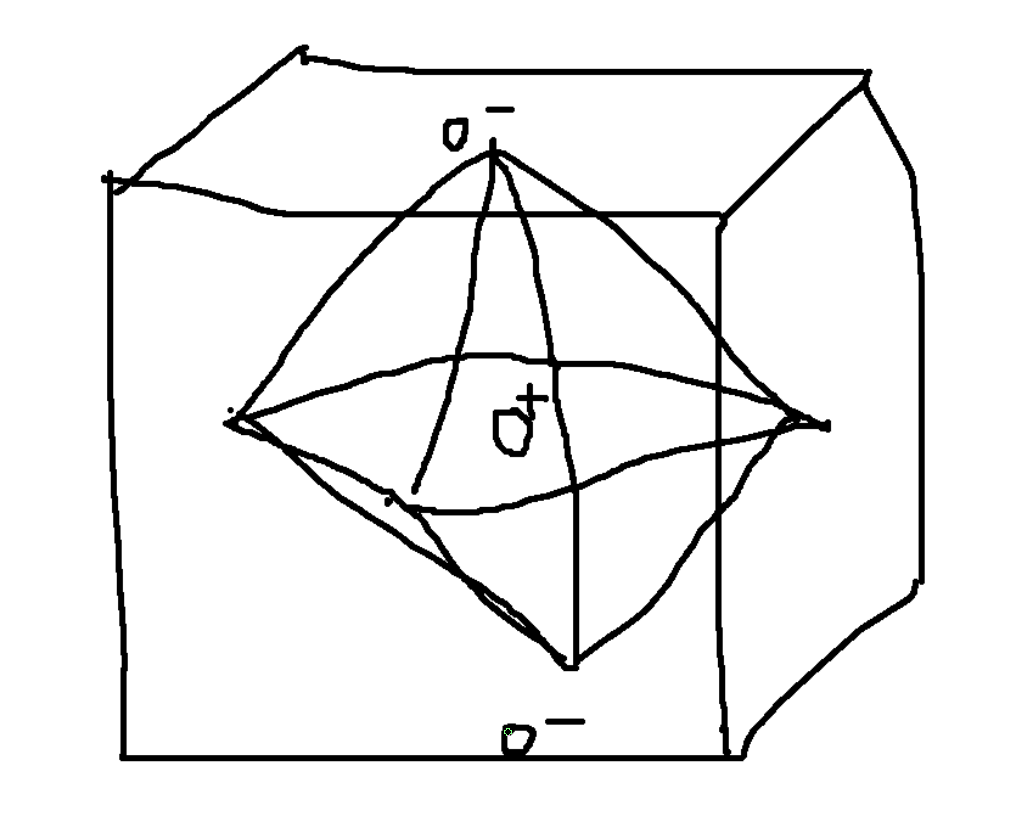
Rotations on a plane: O $_{2} / U (1) \to$ Phase of a complex number. Examples: Easy plane FM, Easy plane AFM, Bose-Einstein condensation (superfluid), various liquid crystal phases. $O_{3}$ rotations in 3D, Heisenberg FM.

Axioms of Group

Set $G$ with binary operatorion $\cdot$ . The group is $(G, \cdot)$ .

$a (b c) = a (b c)$
$a \cdot i = a$
$a \cdot a^{- 1} = i$

Subgroup: Subset $H$ to $G$ , $H$ is a subscrube of $G$ if $(H, \cdot)$ is also a group.

Towards Landau/ Landau-Gurburg Theory

$F (ϕ (x)) = \int d \overset{―}{x} f (n (\overset{―}{x}))$

Consider if we have an ideal gas. Subdivide the space into boxes of size $Δ V$ . Then for $n_{j}$ points in the box at position ${\vec{x}}_{j}$ we have the density, $ρ ({\vec{x}}_{j}) = \frac{n_{j}}{Δ V}$ .

Consider a spatially inhomogenous system. (Ideal gas) with free energy $F (T, V, N) = N k T (\ln (n λ^{3}) - 1)$ . $N_{j} = n ({\vec{x}}_{j}) Δ (V)$ . $f^{i g} = \frac{F (T, V, N)}{Δ V} = n ({\vec{x}}_{j}) k T (\ln (n ({\vec{x}}_{j}) λ^{3}) - 1)$ $n (x), F [n] = \int f (n (x)) d x$ . We integrated out microscopic degrees of freedom and replaced with coarse-grained field. Can calculate any equilibrium property that can be written in terms of $n (x)$ . So, what is $p (n (x)) = ?$ . From before, $α \to p_{α} (H)$ . $n (x) \to p (n (x))$ which is governed by the free energy $F$ of the densities. $p (n (x)) = \frac{1}{Z} \exp (- β F [n (x)])$ . Driving force (to equilibrium)? $μ = \frac{\partial F}{\partial N} = \frac{\partial F / V}{\partial N / V} = \frac{\partial f}{\partial n}$ . Then $μ (x) = \frac{δ F [n (y)]}{δ n (x)} = \frac{δ}{δ n (x)} \int f (n (y)) d y$ , which is called the variational/ functional derivative. Then, $μ (x) = k T \ln (n λ^{3})$ .

Considering currents. $j = n \cdot v$ , $v \propto \frac{\partial μ}{\partial x}$ , $v = - γ \frac{\partial μ}{\partial x}$ . $γ$ relates to mobility and the negative relates to downhill. So, $v = - γ n (x) \frac{\partial k T \ln (n (x) λ^{3})}{\partial x} = - γ n (x) k T \frac{1}{n} \frac{\partial n}{\partial x}$ . From the continuituy equation, $\nabla \cdot J + \frac{\partial n}{\partial t} = 0$ . Putting this together we get $\frac{\partial n}{\partial t} = γ k T \frac{\partial^{2} n}{\partial x^{2}}$ .

$F = \int d x f (T, ⟨ ϕ (\overset{―}{x})) + \int d x \frac{1}{2} k (\nabla ⟨ ϕ (x) ⟩^{2})$ . Landau’s theory: ignore the second term. Including the second term is L-G.

So expanding, $f (T, ϕ) = f_{0} (T) + f_{1} ϕ + f_{2} ϕ^{2} + f_{3} ϕ^{3} + f_{4} ϕ^{4} + \dots$ where the coefficients $f$ can depend on temperature, except:

Highest power of $ϕ$ provides a bounding potential: $ϕ^{2 n}, f_{2 n} > 0$ . So that the order parameter remains finite.
$f_{1}$ : example $ϕ = m = \frac{M}{V}$ . $F (T, V, M) \Rightarrow d F = - S d T - p d V + B d M$ $\frac{\partial F}{\partial M} = \frac{\partial f}{\partial m} = B$ . For high temperature and no field, the magnetization should be zero, hence $ϕ = 0$ . Then, $\frac{\partial f}{\partial m} |_{m = 0} = 0$ since it is a free energy minimum. Therefore, $f_{1} = 0$ . Hence: $f (T, ϕ) = f_{0} (T) + f_{2} ϕ^{2} + f_{3} ϕ^{3} + f_{4} ϕ^{4} + \dots$ . $f (T, ϕ) \equiv$ Landau free energy density. This is typically written: $f = f_{0} (T) + \frac{1}{2} μ (T) ϕ^{2} + \frac{1}{3!} f_{3} ϕ^{3} + \frac{1}{4!} g ϕ^{4}$ by theorists and partical physics. $f = f_{0} (T) + \frac{1}{2} r ϕ^{2} - w ϕ^{3} + u ϕ^{4}$ . $f = f_{0} (T) + \frac{1}{2} b (T) ϕ^{2} + \frac{1}{3} c (T) ϕ^{3} + \frac{1}{4} d ϕ^{4}$ .

Aside: MFT gives qualitative pictures that are pretty accurate to expectation.

Landau Model for Neumatic to Isotropic

Phase transition in liquid crystals.

Isotropic: any orientation of liquid crytals. Neumatic: molecules predominantly align with some axis $\hat{n}$ .

Tensor Model - Neumatic to Isotropic Phase Transition in Liquid Crystal

Let $\hat{n}$ be a global unit vector called the Frank director. Let ${\hat{v}}^{α}$ be the unit director for the $α$ molecule’s orientation.

Ordering is a measure of how close ${\hat{v}}^{α}$ is to $\hat{n}$ , ${\hat{v}}^{α} \cdot \hat{n} = \cos θ$ . For perfect order, $θ = 0, π$ so $\cos^{k} θ$ with $k$ even.

Want $f = f_{0} + f_{1} ϕ + f_{2} ϕ^{2} + f_{3} ϕ^{3} + f_{4} ϕ^{4}$ .

In the high-temperature phase, $f_{1} = 0$ .

Let $Q$ be a tensor. Then, $ϕ^{n} = Tr {Q^{n}}$ . In high T phase $\to ϕ (h i g h) = 0$ . So, $Tr {Q} = 0$ for high temperature. So our outer product, $\vec{v} \cdot {\vec{v}}^{T}$ . Start with, $Q_{i j} = \sum_{α} v_{i}^{α} v_{j}^{α}$ . So, $Q (\vec{s}) = \frac{1}{\frac{N}{V}} \sum_{α} v_{i}^{α} v_{j}^{α} δ (x - {\overset{―}{x}}^{α})$ . Note the tensor must be symmetric.

Absolute disorder: $θ$ is uniformly distributed, $\int d Ω S (θ) = 0$ .

Absolute order, $\forall α . {\vec{v}}^{α} ‖ \hat{n}$ .

Choose a coordinate system such that the first basis vector is $\hat{n}$ . So perfect alignment is ${\vec{v}}^{α} = (1 0 0)$ .

In order state, $v^{α T} v^{α} Tr ((\begin{matrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}) + (\begin{matrix} - 1 / 3 & 0 & 0 \\ 0 & - 1 / 3 & 0 \\ 0 & 0 & - 1 / 3 \end{matrix})) = 0$ .

$Tr ((\begin{matrix} S & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}) + (\begin{matrix} - S / 3 & 0 & 0 \\ 0 & - S / 3 & 0 \\ 0 & 0 & - S / 3 \end{matrix})) = Tr (\begin{matrix} 2 / 3 S & 0 & 0 \\ 0 & - 1 / 3 S & 0 \\ 0 & 0 & - 1 / 3 S \end{matrix})$ .

Then, $⟨ Q_{i j} ⟩ = S (n_{i} n_{j} - \frac{1}{3} δ_{i j})$

$\int d Ω S (\cos^{k} θ) = 0 = \int d φ \int d θ \sin θ S (\cos^{k} θ) = 2 π \int d θ \sin θ S (\cos^{k} θ)$ with $S (\cos^{k} θ) = 1$ for $θ = 0, π$ . $S = \frac{1}{2} ⟨ (3 (v^{α} \cdot \hat{n})^{z} - 1) ⟩ = \frac{1}{2} ⟨ (3 \cos^{2} θ^{α} - 1) ⟩$ .

Trace: $Tr Q^{2} = \frac{4}{9} S^{2} + \frac{1}{9} S^{2} + \frac{1}{9} S^{2} = \frac{2}{3} S^{2}$ . Trace: $Tr Q^{3} = \frac{8}{27} S^{3} - \frac{1}{27} S^{3} - \frac{1}{27} S^{3} = \frac{6}{27} S^{3} = \frac{2}{9} S^{3}$ . Trace: $Tr Q^{4} = \frac{16}{81} S^{4} + \frac{1}{81} S^{4} + \frac{1}{81} S^{4} = \frac{18}{81} S^{4} = \frac{2}{9} S^{4}$ .

$f (S) = \frac{1}{2} r S^{2} - w S^{3} + U S^{4}$ .

$\frac{1}{2} r \frac{3}{2} Tr Q^{2} - w \frac{9}{2} (Tr (Q^{3}) + U \frac{9}{2} Tr (Q^{4}))$ .

$S = \frac{1}{2} ⟨ (3 \cos^{2} θ^{α} - 1) ⟩$

20230130110456-statistical_mechanics.org_20230512_114256.png

$L = \int d Q$ , $d Q = T d S$ .

Ising Model Aside

$m^{2} \to m^{4} \to m^{4} m^{2} m^{2} m^{2} m^{4}$ .

$f = f_{0} \neq f_{2} (T) m^{2} + f_{4} m^{4}$ where $f_{4} > 0$ . $f_{2} (T - T_{C})$ . $f_{2} > 0$ for $T > T_{C}$ and $f_{2} < 0$ for \(T

Can approximate $f_{2}$ for $T \to T_{C}$ by a linear approximation, $f_{2} \approx a (T - T_{C})$ .

Functional Aside

C.f. Entropy, $S = - k \sum_{i} p_{i} \ln p_{i} = - k \int d x p (x) \ln p (x)$ , $\frac{\partial S}{\partial p_{i}} = - k (\ln p_{i} + 1) = S [p (x)] = - k (\ln p (x) + 1)$ .

Functional derivatives, for functions $f$ that can be Taylor expanded about $x$ , $\frac{δ F [f (x)]}{δ f (y)} = lim_{ϵ \to 0} \frac{F [f (x) + ϵ δ (x - y)] - F [f (x)]}{ϵ} = lim_{ϵ \to 0} \frac{\int f (x) + ϵ δ (x - y) d x - \int f (x) d x}{ϵ} = lim_{ϵ \to 0} \frac{\int ϵ δ (x - y) d x}{ϵ} = 1$ . In our case, $F [n (x)] = \int f (n (x)) d x$ . So, $\frac{δ F [n (x)]}{δ n (y)} = lim_{ϵ \to 0} \frac{\int f (n (x) + ϵ δ (x - y)) d x - \int f (n (x)) d x}{ϵ} = lim_{ϵ \to 0} \frac{\int (f (n (x)) + \frac{\partial f}{\partial n} (ϵ δ (x - y)) O (ϵ^{2})) d x - \int f (n (x)) d x}{ϵ} = lim_{ϵ \to 0} \frac{\int \frac{\partial f}{\partial n} (ϵ δ (x - y)) d x}{ϵ} = lim_{ϵ \to 0} \int \frac{\partial f (n (x))}{\partial n (x)} (δ (x - y)) d x = \frac{\partial f (n (y))}{\partial n (y)}$ .

To Try: $F [ϕ (x)] = \exp (\int ϕ (x) f (x) d x)$ , then what is the functional derivative $\frac{δ F [ϕ (x)]}{δ ϕ (y)} = \dots = f (y) F [ϕ (x)]$ .

For one with a gradient: $F [n] = \int f (\overset{―}{x}, n (\overset{―}{x}), \nabla n (\overset{―}{x})) d x$ , $\frac{δ F [n]}{δ n (x)} = \frac{\partial f}{\partial n} - \nabla \cdot \frac{\partial f}{\partial \nabla n}$ .

Aside. For most field theories, we just postulate that $p (ϕ (x)) = \frac{\exp (- β H_{I G} (ϕ (x)))}{Z}$ exists but we can show it for a few. $Z = \int (D ϕ) \exp (- β H (ϕ))$ .

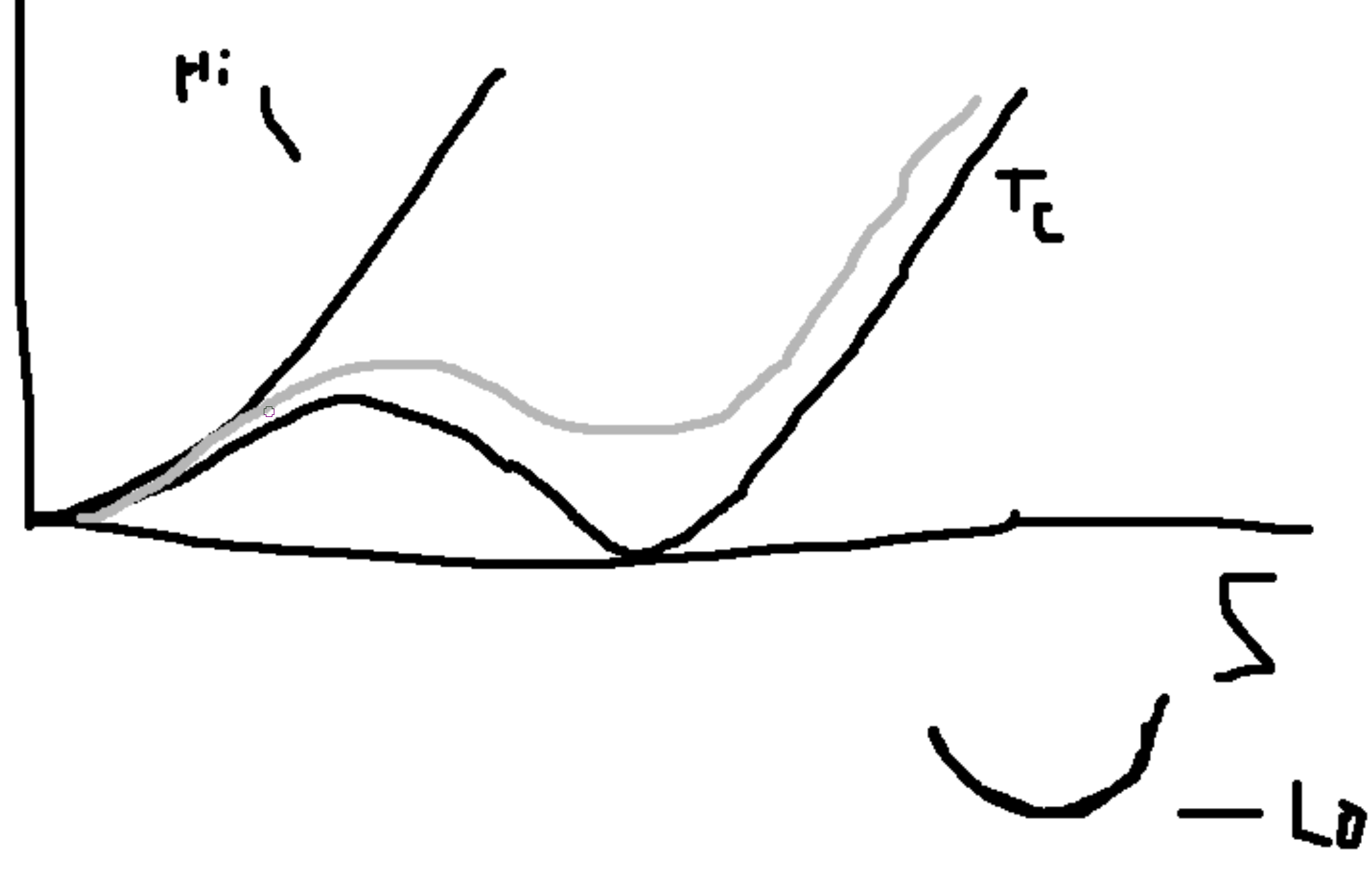
Multicritical Points

$f = \frac{1}{2} r ϕ^{2} + u_{4} ϕ^{4}$ , $u_{4} > 0$ .

When $r$ changes sign you get a continuous phase transition.

Consider the model, $f = \frac{1}{2} r ϕ^{2} + u_{4} ϕ^{4} + u_{6} ϕ^{6}$ , $u_{6} > 0$ and $u_{4}$ can be either sign. Plotting $r$ versus $u_{4}$ ,