Identical Particles

Collide two particles, 1 and 2. If we have a detector $\mathcal{D}$ which detects the particles after the collision. Did it detect 1, 2, or both? Exchange-degeneracy.

We have particle 1 at $x=a$ and particle 2 at $x=b$. If they are distinguishable then exchanging them gives a different setup: $|a_{m_1}{b}_{m_2}⟩\ne |a_{m_2}{b}_{m_1}⟩$. If they are indistinguishable then exchanging them gives the same setup: $|a_{m_1}{b}_{m_2}⟩=|a_{m_2}{b}_{m_1}⟩$.

Given $N$ particles and $N$ boxes then we have $N!$ possible combinations to fill the boxes.

Given $N$ particles and $k$ boxes then we have $\frac{N!}{(N-k)!}=k!(\genfrac{}{}{0ex}{}{N}{k})$ possible permutations to fill the boxes.

How many $k-$combinations can we get? With combinations the boxes are unlabled hence ab and ba are the same. Then we have $(\genfrac{}{}{0ex}{}{N}{k})$.

Note: $(x+y{)}^N=\sum _{k=0}^N(\genfrac{}{}{0ex}{}{N}{k})x^k{y}^{N-k}$.

$E_{tot}=\frac{{\hslash }^2{\pi }^2}{m{L}^2}$. For each particle, $\frac{{\hslash }^2{\pi }^2}{2m{L}^2}(n_1^2+n_2^2)$. Then, we have $|11⟩$ which is allowed for distinguishable and bosonic particles.

$E_{tot}=\frac{5{\hslash }^2{\pi }^2}{2m{L}^2}$. For each particle, $\frac{{\hslash }^2{\pi }^2}{2m{L}^2}(n_1^2+n_2^2)$. Then, we have $|12⟩,|21⟩$ which is allowed for distinguishable. Boson: $1/\sqrt{2}(|12⟩+|21⟩)$. Fermion: $1/\sqrt{2}(|12⟩-|21⟩)$.

For more degrees of freedom, say spin, then a symmetric function would be both the coordinate and spin being symmetric or antisymmetric.

We will not consider relativisitic corrections, and have spin-dependent terms and a stationary nucleus.

\(H = \sum_i^Z \frac{p_i^2}{2m} - \sum_i^Z \frac{Ze^2}{R_i} + \sum_{i

If we didn’t have the last term, $H=\sum _i^Z{H}_i$. Hence, $\mathrm{\Psi }={\mathrm{\Psi }}_1\cdots {\mathrm{\Psi }}_Z$.

How many terms does the last term have? $\frac{Z(Z-1)}{2}=(\genfrac{}{}{0ex}{}{Z}{2})$ terms.

The second term is roughly, $\frac{Z{e}^2}{R}Z$ and the third is roughly $\frac{e^2}{R}\frac{Z(Z-1)}{2}$.

The second term is 4 times larger for helium, not a great perturbation. As we increase $Z$, we approach 2, which is definitely a great perturbation.

$H_0\mathrm{\Psi }=E\mathrm{\Psi }$, $H_0=H_1+H_2$, $H=\frac{p_1^2}{2m}+\frac{p_2^2}{2m}+\frac{e^2}{|{\overrightarrow{R}}_1-R_2|}-\frac{2e^2}{R_1}-\frac{2e^2}{R_2}=H_0+V_p$, $E=E_1^{n_1{\ell }_1}+E_2^{n_2{\ell }_2}$. Then, $H_0=\frac{p_1^2}{2m}+\frac{p_2^2}{2m}+V_c(R_1)+V_c(R_2)$.

Degeneracy:

1. $n_1\ne n_2\vee {\ell }_1\ne {\ell }_2$: $4(2{\ell }_1+1)(2{\ell }_2+1)$
2. $n_1=n_2\wedge {\ell }_1={\ell }_2$: $(2\ell +1)(4\ell +1)$

If we had a $1s^2$ state then we would have $|\mathrm{\Psi }⟩=\frac{1}{\sqrt{2}}{\mathrm{\Psi }}_{n_1{\ell }_1{m}_1}(|+-⟩-|-+⟩)|100;100⟩={\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_2)\frac{1}{\sqrt{2}}(|+-⟩-|-+⟩)$. Spatial antisymmetric and spin symmetric OR Spatial symmetric and spin antisymmetric. The spin antisymmetric is only possible for the same spatial quantum numbers.

$V_p=-\frac{2e^2}{R_1}-\frac{2e^2}{R_2}+\frac{e^2}{|{\overrightarrow{R}}_1-{\overrightarrow{R}}_2|}-V_c(R_1)-V_c(R_2)$.

Consider the 1s + 2s configuration. For our 4-fold degenerate space, we must find the 4 wavefunctions. ${|}^{1}S⟩=|{\mathrm{\Psi }}_{spatial,S}⟩\otimes |{\mathrm{\Psi }}_{spin,A}⟩={\mathrm{\Psi }}_S\otimes |s=0,m_S=0⟩={\mathrm{\Psi }}_S\otimes |0,0⟩={\mathrm{\Psi }}_S\otimes \frac{1}{\sqrt{2}}(|+-⟩-|-+⟩)$. ${|}^{2}S⟩=|{\mathrm{\Psi }}_{spatial,A}⟩\otimes |{\mathrm{\Psi }}_{spin,S}⟩=\frac{1}{\sqrt{2}}(|100;200⟩-|200;100⟩)\otimes \{\begin{array}{l}|10⟩\\ |11⟩\\ |1-1⟩\end{array}$.

So, $⟨\mathrm{\Psi }|V|\mathrm{\Psi }⟩=⟨{\mathrm{\Psi }}_{spatial}|V|{\mathrm{\Psi }}_{spatial}⟩$. Note that the spin is unperturbed by our potential. From the spins, we see that our perturbation is already diagonal. I will call our two spatial wavefunctions by the spectroscopic notation. ${⟨}^{1}S|V{|}^{1}S⟩,{⟨}^{3}S|V{|}^{3}S⟩$.

Then, $⟨V⟩=\frac{1}{2}[\int d^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2|{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){|}^{2}V|{\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_2){|}^2+\int d^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2|{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_2){|}^{2}V|{\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_1){|}^2\pm \int d^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2{\mathrm{\Psi }}_{1s}^{\ast }({\overrightarrow{r}}_1){\mathrm{\Psi }}_{2s}^{\ast }({\overrightarrow{r}}_2)V{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_2){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_1)\pm \int d^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2{\mathrm{\Psi }}_{1s}^{\ast }({\overrightarrow{r}}_2){\mathrm{\Psi }}_{2s}^{\ast }({\overrightarrow{r}}_1)V{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_2)]=\int d^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2|{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){|}^{2}V|{\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_2){|}^2\pm \int d^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2{\mathrm{\Psi }}_{1s}^{\ast }({\overrightarrow{r}}_1){\mathrm{\Psi }}_{2s}^{\ast }({\overrightarrow{r}}_2)V{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_2){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_1)$. Note that $V$ has five terms so we get a trivial 10 integrals to evaluate.

Consider the first integral.

$$\begin{array}{rl}\int d^6\overrightarrow{r}|{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){|}^{2}V|{\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_2){|}^2& =-2e^2(\int d^3{\overrightarrow{r}}_1\frac{|{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){|}^2}{r_1}+\int d^3{\overrightarrow{r}}_2\frac{|{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_2){|}^2}{r_2})\\ & +e^2\int d^6\overrightarrow{r}\frac{|{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){|}^2|{\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_2){|}^2}{|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2|}\\ & -\int d^3{\overrightarrow{r}}_1|{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){|}^2{V}_c(r_1)-\int d^3{\overrightarrow{r}}_2|{\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_2){|}^2{V}_c(r_2)\\ & =-2e^2{I}^{\prime }+e^2{K}^{\prime }-I_1-I_2=I+K-I_1-I_2.\end{array}$$

The cross terms,

$$\begin{array}{rl}\int d^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2{\mathrm{\Psi }}_{1s}^{\ast }({\overrightarrow{r}}_1){\mathrm{\Psi }}_{2s}^{\ast }({\overrightarrow{r}}_2)V{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_2){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_1)& =-2e^2(\int d^3{\overrightarrow{r}}_1\frac{{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_1)}{r_1}\int d^3{\overrightarrow{r}}_2{\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_2){\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_2)+\int d^3{\overrightarrow{r}}_2\frac{{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_2){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_2)}{r_2}\int d^3{\overrightarrow{r}}_1{\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_1){\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1))(=0)\\ & +e^2\int d^6\overrightarrow{r}\frac{{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_2){\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_2){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_1)}{|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2|}\\ & -\int d^3{\overrightarrow{r}}_1{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_1)V_c(r_1)\int d^3{\overrightarrow{r}}_2{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_2){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_2)-\int d^3{\overrightarrow{r}}_1{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_1)V_c(r_1)\int d^3{\overrightarrow{r}}_1{\mathrm{\Psi }}_{1s}({\overrightarrow{r}}_1){\mathrm{\Psi }}_{2s}({\overrightarrow{r}}_1)\\ & =-2e^{2}0+e^2{J}^{\prime }-0-0=J.\end{array}$$

Note that $I_1,I_2$ are average energy for the central field for each electron. $J$ is the exchange integral and is purely Quantum Mechanical.

Therefore, our full energies are $E_{+}=I-I_1-I_2+K+J$ and $E_{-}=I-I_1-I_2+K-J$. Thus, we get a 4-fold degeneracy split into 1-fold and 3-fold degeneracy split by the exchange interaction.

So, if $V_c(r_i)=-\frac{2e^2}{r_i}$ then $V=\frac{e^2}{|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2}$ and $I-I_1-I_2=0$, Energies become $K\pm J$. But note that this only contributes to an energy shift, not the split.

The singlet state has the higher energy, $E_{+}$ since it is the symmetric spin wavefunction. The triplet state has the higher energy, $E_{-}$ since it is the antisymmetric spin wavefunction.

In the context of helium, the singlet state is called parahelium and the triplet is orthohelium.

Consider 2 hydrogen nuclei (a,b) with an electron each (1,2).

So, ${\overrightarrow{r}}_{a1}$ is the vector between nucleus a and electron 1. Our total set of vectors are: ${\overrightarrow{r}}_{a1},{\overrightarrow{r}}_{a2},{\overrightarrow{r}}_{ab},{\overrightarrow{r}}_{b1},{\overrightarrow{r}}_{b2},{\overrightarrow{r}}_{12}$.

The Hamiltonian is then, $-\frac{{\hslash }^2}{2m_e}({\mathrm{\nabla }}_1^2+{\mathrm{\nabla }}_2^2)+e^2\frac{1}{r_{12}}-e^2(\frac{1}{{\overrightarrow{r}}_{a1}}+\frac{1}{{\overrightarrow{r}}_{a2}}+\frac{1}{{\overrightarrow{r}}_{b1}}+\frac{1}{{\overrightarrow{r}}_{b2}})$ Let $r_{ab}$ be a parameter of the system.

If $r_{ab}\to \mathrm{\infty }$ then $H_{a1}=-\frac{{\hslash }^2}{2m_e}{\mathrm{\nabla }}_1^2-\frac{e^2}{r_{a1}},H_{b2}=-\frac{{\hslash }^2}{2m_e}{\mathrm{\nabla }}_2^2-\frac{e^2}{r_{b2}}$. Thus, $H_0=H_{a1}+H_{b2}$. The perturbation is then, $V=\frac{e^2}{r_{12}}-e^2(\frac{1}{r_{a2}}+\frac{1}{r_{b1}})$.

So, $H_0{\mathrm{\Psi }}_1=E_0{\mathrm{\Psi }}_1$, ${\mathrm{\Psi }}_1={\mathrm{\Psi }}_a({\overrightarrow{r}}_{a1}){\mathrm{\Psi }}_b({\overrightarrow{r}}_{b2})$. Then, $H_0{\mathrm{\Psi }}_1=E_0{\mathrm{\Psi }}_1=2E_I{\mathrm{\Psi }}_1$.

The exchanged hamiltonian is then $H_0^{\prime }=H_{a2}+H_{b1}$. $H_{a2}=-\frac{{\hslash }^2}{2m}{\mathrm{\nabla }}_2^2-\frac{e^2}{r_{a2}},H_{b1}=\cdots$. Then, ${\mathrm{\Psi }}_2={\mathrm{\Psi }}_a({\overrightarrow{r}}_{a2}){\mathrm{\Psi }}_b({\overrightarrow{r}}_{b1})$ with the same energy, $H_0^{\prime }{\mathrm{\Psi }}_2=2E_I{\mathrm{\Psi }}_2$.

Then the full Hamiltonian is $H=H_0+V_{a1,b2}=H_0^{\prime }+V_{a2,b1}$.

Our full wavefunction is then $c_1{\mathrm{\Psi }}_1+c_2{\mathrm{\Psi }}_2+\varphi$. Note that we will show $|c_2|=|c_1|$.

$H_1\mathrm{\Psi }=E\mathrm{\Psi }=(2E_I+\mathrm{\Delta }E)\mathrm{\Psi }$.

$$\begin{array}{rl}\text{(1)}& c_{1}H{\mathrm{\Psi }}_1+C_{2}H{\mathrm{\Psi }}_2+H\varphi & =(2E_1+\mathrm{\Delta }E)(c_1{\mathrm{\Psi }}_1+c_2{\mathrm{\Psi }}_2+\varphi )c_1{V}_{a1,b2}{\mathrm{\Psi }}_1+c_2{V}_{a2,b1}{\mathrm{\Psi }}_2+H\varphi & =2E_1\varphi +(\mathrm{\Delta }E)(c_1{\mathrm{\Psi }}_1+c_2{\mathrm{\Psi }}_2+\varphi )\\ \text{(2)}& c_1{V}_{a1,b2}{\mathrm{\Psi }}_1& =\mathrm{\Delta }E{c}_1{\mathrm{\Psi }}_1\text{(3)}& c_2{V}_{a2,b1}{\mathrm{\Psi }}_2& =\mathrm{\Delta }E{c}_2{\mathrm{\Psi }}_2\text{(4)}& H\varphi & =(2E_1+\mathrm{\Delta }E)\varphi \end{array}$$

Reducing by neglecting second-order perturbation,

$$\begin{array}{}\text{(5)}& c_1{V}_{a1,b2}{\mathrm{\Psi }}_1& =\mathrm{\Delta }E{c}_1{\mathrm{\Psi }}_1\text{(6)}& c_2{V}_{a2,b1}{\mathrm{\Psi }}_2& =\mathrm{\Delta }E{c}_2{\mathrm{\Psi }}_2\text{(7)}& H_0\varphi =H_0^{\prime }\varphi & =2E_1\varphi \end{array}$$

Then,

$$\begin{array}{}\text{(8)}& (H_0-2E_I)\varphi & =(\mathrm{\Delta }E-V_{a1,b2})c_1{\mathrm{\Psi }}_1+(\mathrm{\Delta }E-V_{a2,b1})c_2{\mathrm{\Psi }}_2.\end{array}$$

Note the RHS is the inhomogeneity. If RHS is zero then, $H_0\varphi -2E_1\varphi \Rightarrow \varphi ={\mathrm{\Psi }}_1$ if $H_0$ and $\varphi ={\mathrm{\Psi }}_2$ if $H_0^{\prime }$.

For an inhomogenous equation, there is a solution only if the RHS is orthogonal to the solution of the homogenous equation. Then,

$$\begin{array}{}\text{(9)}& \int [(\mathrm{\Delta }E-V_{a1,b2})c_1{\mathrm{\Psi }}_1+(\mathrm{\Delta }E-V_{a2,b1})c_2{\mathrm{\Psi }}_2{]}^{\ast }{\mathrm{\Psi }}_1{d}^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2& =0\text{(10)}& \int [(\mathrm{\Delta }E-V_{a1,b2})c_1{\mathrm{\Psi }}_1+(\mathrm{\Delta }E-V_{a2,b1})c_2{\mathrm{\Psi }}_2{]}^{\ast }{\mathrm{\Psi }}_2{d}^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2& =0\end{array}$$

Let,

$$\begin{array}{}\text{(11)}& K& =\int V_{a1,b2}|{\mathrm{\Psi }}_1{|}^2{d}^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2\text{(12)}& K& =\int V_{a2,b1}|{\mathrm{\Psi }}_2{|}^2{d}^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2\text{(13)}& \mathrm{\Delta }E& =\int \mathrm{\Delta }E|{\mathrm{\Psi }}_{1,2}{|}^2{d}^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2\text{(14)}& 0>J& =\int V_{a2,b1}{\mathrm{\Psi }}_2^{\ast }{\mathrm{\Psi }}_1{d}^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2\text{(15)}& 0>J& =\int V_{a1,b2}{\mathrm{\Psi }}_1^{\ast }{\mathrm{\Psi }}_2{d}^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2\end{array}$$

Gives us,

$$\begin{array}{}\text{(16)}& \mathrm{\Delta }E{c}_1-c_{1}K+\mathrm{\Delta }E{c}_2\int {\mathrm{\Psi }}_2^{\ast }{\mathrm{\Psi }}_1{d}^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2-c_{2}J& =0\text{(17)}& \mathrm{\Delta }E{c}_1-c_{1}K+\mathrm{\Delta }E{c}_2|s{|}^2-c_{2}J& =0\text{(18)}& \mathrm{\Delta }E{c}_2-c_{2}K+\mathrm{\Delta }E{c}_1\int {\mathrm{\Psi }}_1^{\ast }{\mathrm{\Psi }}_2{d}^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2-c_{1}J& =0\mathrm{\Delta }E{c}_2-c_{2}K+\mathrm{\Delta }E{c}_1|s{|}^2-c_{1}J& =0\end{array}$$

So,

$$\begin{array}{}\text{(19)}& {\mathrm{\Psi }}_1^{\ast }{\mathrm{\Psi }}_2{d}^3{\overrightarrow{r}}_1{d}^3{\overrightarrow{r}}_2& =\int {\mathrm{\Psi }}_a^{\ast }({\overrightarrow{r}}_{a1}){\mathrm{\Psi }}_b({\overrightarrow{r}}_{b1})d^3{\overrightarrow{r}}_1\int {\mathrm{\Psi }}_b^{\ast }({\overrightarrow{r}}_{b2}){\mathrm{\Psi }}_a({\overrightarrow{r}}_{a2})d^3{\overrightarrow{r}}_2\text{(20)}& & =S{S}^{\ast }\text{(21)}& & =|S{|}^2.\end{array}$$

Gives us,

$$\begin{array}{}\text{(22)}& [\mathrm{\Delta }E-K]c_1+[\mathrm{\Delta }E|S{|}^2-J]c_2& =0\text{(23)}& [\mathrm{\Delta }E-K]c_2+[\mathrm{\Delta }E|S{|}^2-J]c_1& =0.\left|\begin{array}{cc}\mathrm{\Delta }E-K& \mathrm{\Delta }E|S{|}^2-J\\ \mathrm{\Delta }E|S{|}^2-J& \mathrm{\Delta }E-K\end{array}\right|& =0\text{(24)}& (\mathrm{\Delta }E{)}_1& =\frac{K+J}{1+|S{|}^2}\text{(25)}& (\mathrm{\Delta }E{)}_2& =\frac{K-J}{1+|S{|}^2}.\end{array}$$

The second is the symmetric solution $c_1=c_2$.

${\mathrm{\Psi }}_{S,Spatial}=\frac{1}{\sqrt{2(1+|S{|}^2)}}({\mathrm{\Psi }}_1+{\mathrm{\Psi }}_2)$. Then, $E_S=2E_1+\frac{e^2}{r_{ab}}+\frac{K-J}{1+|S{|}^2}=2E_1+\frac{e^2}{r_{ab}}+K+J-|S{|}^2\frac{K+J}{1+|S{|}^2}$, which also includes the proton-proton energy. The second form is written so that you can treat the last term as a small correction.

${\mathrm{\Psi }}_{A,Spatial}=\frac{1}{\sqrt{2(1-|S{|}^2)}}({\mathrm{\Psi }}_1-{\mathrm{\Psi }}_2)$. $E_A=2E_1+\frac{e^2}{r_{ab}}+\frac{K+J}{1+|S{|}^2}=2E_1+\frac{e^2}{r_{ab}}+K-J-|S{|}^2\frac{K-J}{1-|S{|}^2}$. Thus, the exchange energy is the differentiating factor and since $J<0$ the antisymmetric wavefunction is higher energy.

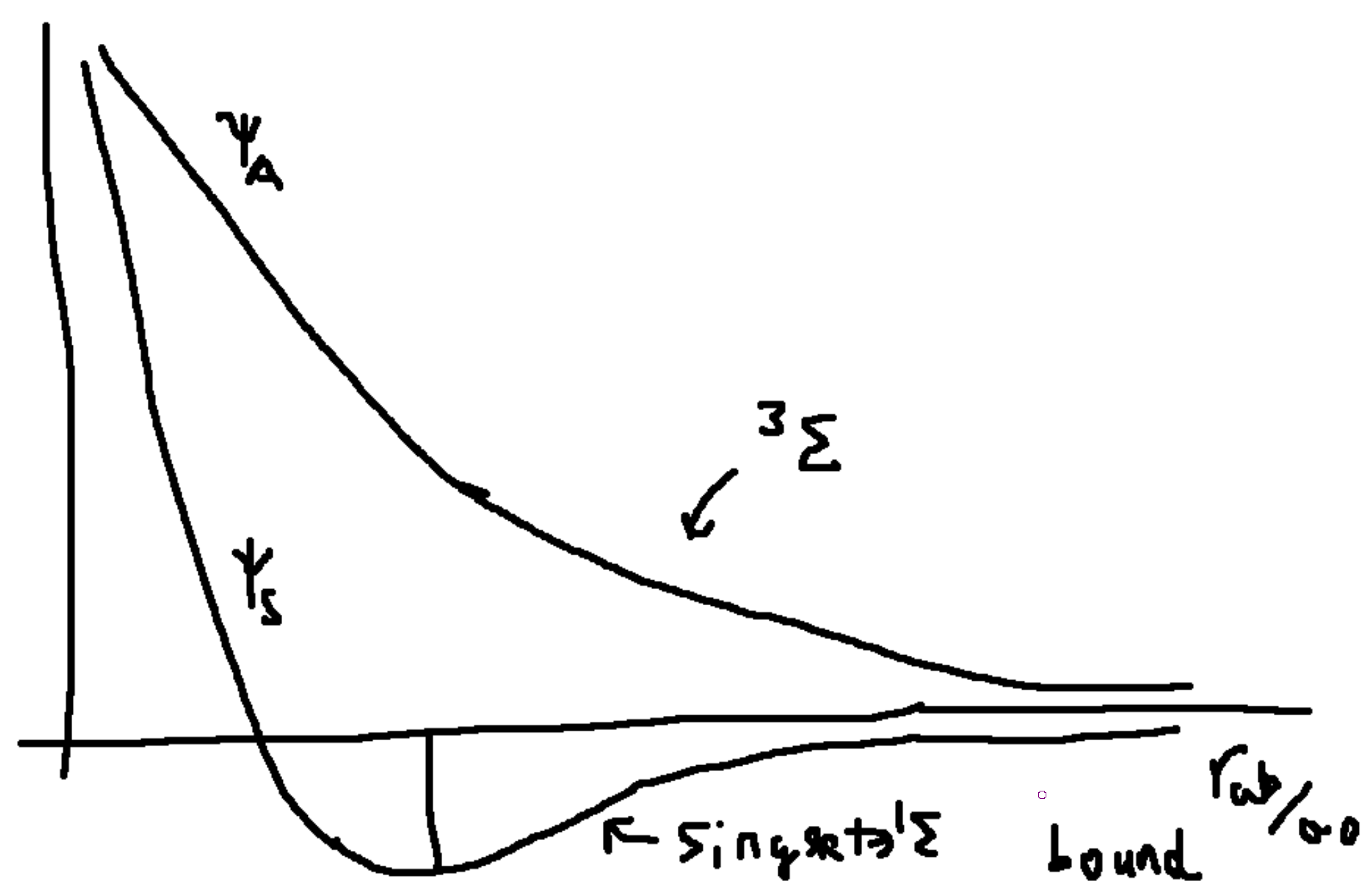
Bond length: $r_{ab,0}\approx 1.4a_0$, where the verticle reaches the x-axis. The bottom of the well is like a harmonic oscillator with $\frac{\hslash {\omega }_0}{2}$ given by the curvature of the bottom of the well: ${\omega }_0=\sqrt{\frac{1}{m}\frac{d^3{E}_S}{d{r}_{ab}^2}}$. The height is the Diassociation energy $D=4.38$ eV.

	Theory	Experiment
$r_{ab}$	0.735 A	0.753 A
${\omega }_0$	4280 1/cm	4390 1/cm
$D$	4.37 eV	4.38 eV