Thermodynamics

Note: Intensive dExtensive Hence, $d U = T d S + P d V + μ d N$ .

Extensive means $f (a A, a B, a C) = a f (A, B, C)$

Definitions

Systems

Consists of many constituents (particles) $N ≫ 1$ . Macroscopic.

We also wait long enough for the system it arrives to its thermodynamic (TD) equilibrium state.

If it is in the TD equilibrium state then it can be described by a few physical quantities called state variables.

Example of state variables: $N, V, P, U, μ, τ, L, σ, A, T$ . (3D: PV, 1D: $τ$L, 2D: $σ$A) All have physical meaning except temperature $T$ which is defined in its relation to the others.

$d W = {τ d x, σ d A, - p d V, μ d N, B d μ E d P}$ . We call the first term (p) the generalized force (intensive) and the second term (dV) the generalized displacement (extensive) and we call them both together conjugate pairs.

Temperature

Specifically, Temperature describes the process of energy exchange between different systems in thermal contact.

Energy flows (is transfered) from the system with high temperature to the system with low temperature.

The systems reach thermal equilibrium when no more net energy transfer takes place by heating or cooling and at this point their temperatures are equal.

Unit: [T] = K, Kelvin with $T > 0$ .

Boltzmann Constant

$k_{B} = 1.38 \cdot 10^{- 23} \frac{J}{K}$ . So the units [ $k_{b} T$ ]=[energy].

The equation of state (EOS) is a functional relationship between the state variables of a system (in TD equilibrium).

EOS can be obtained experimentally, ex. ideal gas law, $p V = N k_{B} T$ (dilute gas) which has a 200yr history.

Also can be obtained from first principles using SM or empirically (approximate). An example is the van der Walls EOS (vdW) $(p + a \frac{N^{2}}{V^{2}}) (V - N b) = N k_{B} T .$

EOS are continuous and small changes in one variable lead to small changes in the other variables unless something dramatic happens (e.g. phase change, where the system fundamentally changes its state [symmetry change/ topology change]). This second part is the well behaved nature of the system. Example solid $\leftrightarrow$ liquid. (Liquids are more fundamental since they have more symmetry [higher temperature generally implies more symmetries])

Small changes implies that you can linearize the EOS. An example from the ideal gas law: $V d p + p d V = k_{B} T d N + N k_{B} d T$ . The $d p, d V$ are called total differentials. vdW EOS describes both liquid and gas but has unphysical regions and requires interpretation.

Types of Equilibrium

Thermal: $T_{A} = T_{B}$
Mechanical: $p_{A} = p_{B}$ , $τ_{A} = τ_{B}$
Chemical/ Diffusive: $μ_{A} = μ_{B}$

Process

A change of a system from one state (A) to another state (B).

Processes can be fast, slow, spontaneous, reversible, irreversible, quasistatic.

Quasistatic

A qs process is usually idealized process where all relevant state variables are well defined for the entire process.

In other words, a qs process is a sequence of TD equilibrium states.

Laws

Zeroth Law of TD

If A is in thermal equilibrium with C and B is in equilibrium with C then A is in thermal equilibrium with B.

First Law

Energy is conserved (provided we include energy changes by doing work and heating).

$Δ U = W + Q$ for Finite changes and always true.

$d U = d Q + d W$ where d means small and $d U$ is a total differential and this expression is always true.

Then, $d U = d Q - p d V + μ d N = T d S - p d V + μ d N$ ( $d Q = T d S$ for Quasistatic Processes and is not always true).

Real Process $↛$ quasistatic (idealized) process.

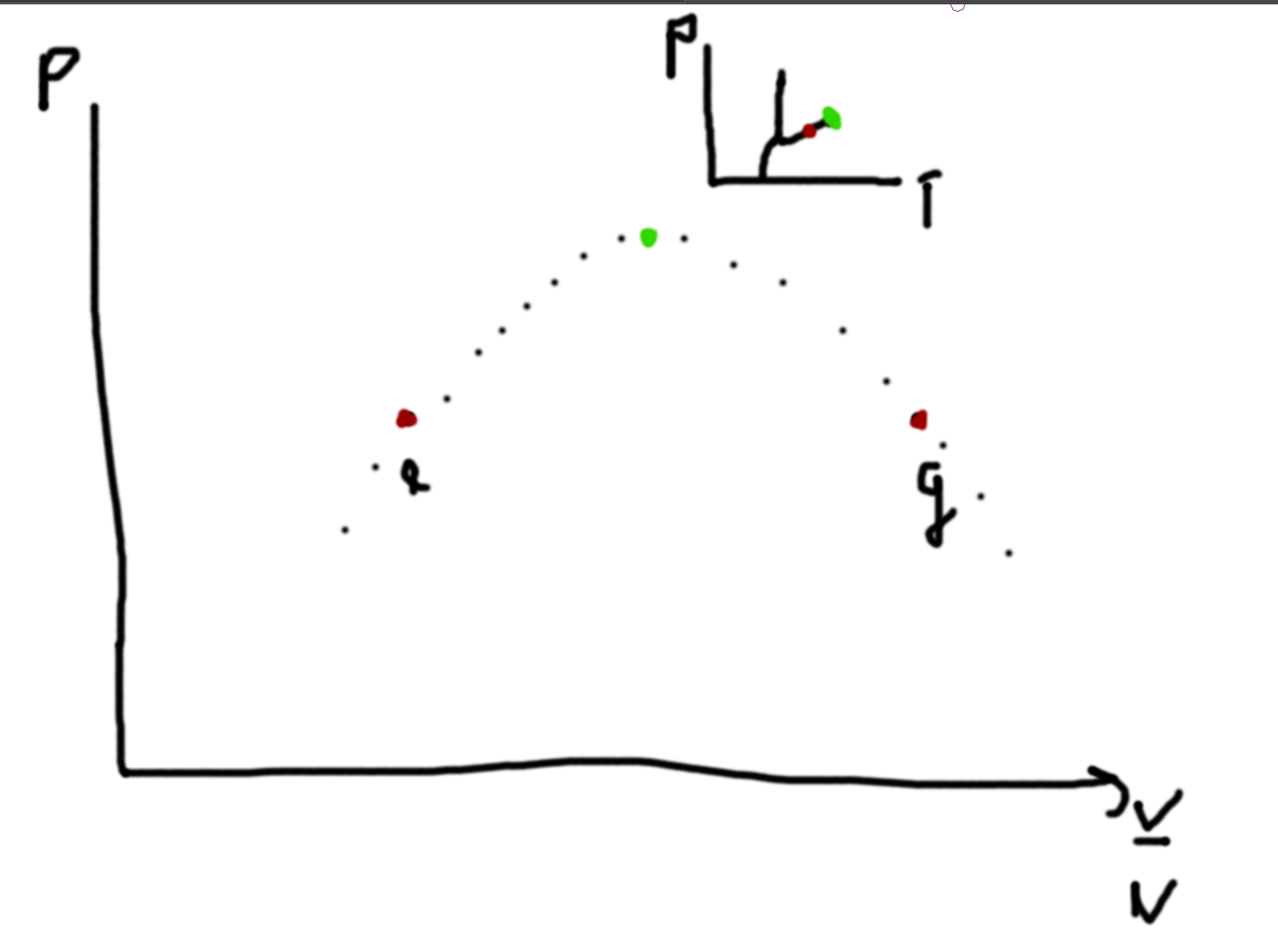
Example - Gasoline 4 stroke Engine

Expand Volume (ignite and expand)
Explosion
Intake
Compression

1–2 Q=0 3–4 Q=0 2–4 dV=0 3–1 dV=0

20230111105947-thermodynamics.org_20230117_131553.png

Ideal Gas

$p V = N k T$ , $U \propto N k T$ .

Processes

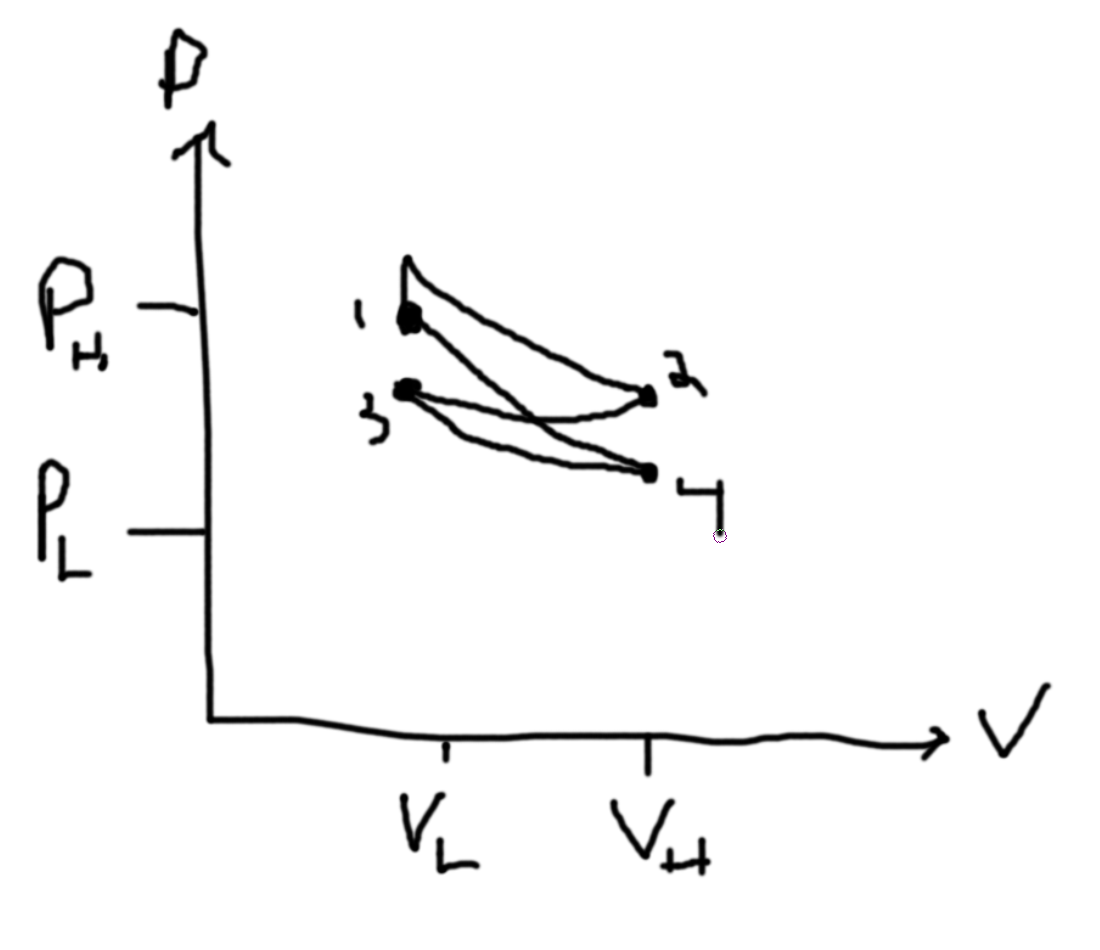
What is the sign of the entropy changes? V2 is initially empty.

(A) Slow Expansion (environment has temperature T1 and gas is in piston environment with pressure P1 and volume V1 and gets expanded to 2V1 = V2)
(B) Remove pin holding boundary between two volumes
(C) Small Hole in Boundary between two volumes
(D) Thermally insulated adiabatic wall (expand slowly)

Questions to ask - Systemitize
1. Is the process quasistatic? (A,D due to them being slow) (B is not due to it being fast) (C is not a sequence of equilibrium states and so it is not)
2. Use First Law (ΔU = W + Q)
3. Find initial and final states for (ΔU, W, Q)
4. Find quasistatic process that have the same initial and final states to analysize the non-qs processes
For (A) there is no change in Energy. For (B) there is no Work. For (C) there is no Work. For (D) there is no Heat Exchange.

For A,B,C the final pressure is half, the final volume is double. Note that ABC has no change in internal energy. Q is zero. W = -Q for A and since work is done by the system, work is negative and so entropy increases. Because BC is not quasistatic (we cannot use dQ = TdS), we can relate them to A and see that entropy must increase. D has Q=0 and so entropy does not change but the temperature decreases since the internal energy decreases (from the fact that the system is doing work).

Systematize

What are the state variables?
How many (total)?
How many are independent?
Which ones are independent?

State Variables

1 energy, 2 state variables for heating, 2 variables for each work. Thus we have a total number of state variables is 1 + 2Nw + 2 state variables. And the number of independent state variables is Nw+1.

Assume we have amystery state variable X, we then assume U(X) so we can find the conjugate pair.

Relations between state variables are described by well behaved EOS (twice differentiated). I.e. small changes are equivalent to toal differentials.

Legendre? Transformation: Let Z=f(X,Y). $d Z = {\frac{d f}{d x} |}_{y} d x + {\frac{d f}{d y} |}_{x} d y$ . Let $g (w, z) = f (x, y)$ then ${(\frac{\partial g}{\partial w})}_{z} d w + {(\frac{\partial g}{\partial z})}_{w} d z = {(\frac{\partial f}{\partial x})}_{y} d x + {(\frac{\partial f}{\partial y})}_{x} d y$ . I.e. convert $U$ to $F$ or $H$ , etc.

I.e. for the internal energy, $d U = {\partial_{S} U |}_{V, N} d S + {\partial_{V} U |}_{S, N} d V + {\partial_{N} U |}_{S, V} d N = T d S - p d V + μ d N$ . Note, that since we have $U(S,V,N) then we have $T (S, V, N) = \frac{\partial U}{\partial S}$ , i.e. a function of the same variables, and similarly for $V, N$ . Also, using this equivalence between the partial of the internal energy and the temperature, pressure, and chemical potential, we can then get $S (T, V, N)$ and thus get $U (T, V, N)$ .

We can look at U(T,V,N). So, $d U = {\frac{\partial U}{\partial T} |}_{V, N} d T + \dots d V + \dots d N$ . Note, that this is not necessarily equal to $S d T - p d V + μ d N$ since we are holding something different constant now. Thus, ${\frac{\partial U}{\partial V}}_{T, N} \neq - p$ (at least not necessarily).

Consider: $F = U - T S$ . Then $d F = d U - {\frac{\partial (T S)}{\partial T} |}_{S, U} d S - {\frac{\partial (T S)}{\partial S} |}_{T, U} d S = d U - S d T - T d S = T d S - p d V + μ d N - S d T - S d T = - S d T - p d V + μ d N$ .

Energies

U(S,V,N) (Assume: S(U,V,N), V(U, S, N), N(U, S, V), we may also write ℐ(U,S,V,N)=0)
F = U - TS : F(T,V,N)
H = U+PV : H(S,P,N)
G = U - TS + PV : G(T,P,N)
𝓖 = U - TS - μN : 𝓖(T,P,μ)

Note from $S (U, V, N)$ then $d S = \frac{1}{T} d U + \frac{P}{T} d V - \frac{μ}{T} d N$ .

For Heating and Work

Heating: S, T
Work: (P,V), (μ, N), (B, μ), …

Response Functions

Notes

Compressibility: $κ_{S o r T} = - \frac{1}{V} {(\frac{\partial V}{\partial p})}_{S o r T} > 0$ (we will show the greater than later)
Thermal Expansion: $α = \frac{1}{V} {(\frac{\partial V}{\partial T})}_{P}$ can be greater or less than zero.
$\frac{\partial Q}{\partial T}$ - Heat Capacity

Heat Capacity

Entropy Changes from Earlier Examples

Use an ideal gas. $V_{0} \to V_{1} = 2 V_{0}$ . Recall: $U = c N k T$ and $p V = N k T$ .

Slow Isothermal Expansion

From slow, we know quasistatic. $N, T, V$ Want: $S$ . $d U = c N k d T$ . Note, we have $d U = T d S - p d V + μ d N$ . So, since this is isothermal, $d U = 0$ . Then, $T d S = p d V$ . Then, $\int_{S_{0}}^{S_{1}} f (S) d S = \int_{V_{0}}^{V_{1}} g (V) d V$ . So, $d S = \frac{P}{T} d V = \frac{N k}{V} d V$ Then, $Δ S = N k \ln 2$ .

Adiabatic Expansion

Calculate work done. Note $d Q = 0$ .

$d U = C_{v} d T = - p d V$ . $d H = C_{p} d T = V d p$ .

$C_{v} T = N k T \ln (V)$ $C_{p} T = N k T \ln (P)$ $\frac{C_{V}}{C_{p}} = \frac{\ln (V)}{\ln (P)} = γ$ . Thus, $P^{γ} = V$ .

So, $d W = - p d V \Rightarrow W = - \int_{V}^{2 V} p d V$ .

Alternatively (in class): $d U = - p d V = c N k d T$ Then, $p d V + V d p = N k d T$ (4) $P V = N k T$ $p d V + V d p = N K d T$ (from 4). $p d V + V d p = - \frac{P}{c} d V$ $f_{1} (p) d p = f_{2} (V) d V$ .

$p V^{ν} = C$ , $ν = \frac{c + 1}{c}$ .

$W = \int_{V}^{2 V} - p d V$ .

Efficiency

Example Problems

One

$f = g^{2} + h^{2} + ℓ^{2}$ $ℓ = \ln (h - g) + h^{2}$ . Using these two EOS, find ${(\frac{\partial f}{\partial ℓ})}_{h}$ ${(\frac{\partial f}{\partial h})}_{ℓ}$ .

Strategy:

Find the function with the variables mentioned: $f (h, ℓ)$
Linearize, $d f = \partial_{h} f d h + \partial_{ℓ} f d ℓ$ .

Need $f (h, ℓ)$ since we have just those two variables. Then, we want: $d f = {(\frac{\partial f}{\partial h})}_{ℓ} d h = {(\frac{\partial f}{\partial ℓ})}_{h} d ℓ$ . We have: $d f = {(\frac{\partial f}{\partial g})}_{h, ℓ} d g + {(\frac{\partial f}{\partial h})}_{g, ℓ} d h = {(\frac{\partial f}{\partial ℓ})}_{h, g} d ℓ$ . $d ℓ = {(\frac{\partial ℓ}{\partial g})}_{h} d g + {(\frac{\partial ℓ}{\partial h})}_{g} d h$ . Then, $d g$ can be obtained from this expression of $d ℓ$ . So, $d f = [{(\frac{\partial f}{\partial h})}_{g, ℓ} - {(\frac{\partial f}{\partial g})}_{h, ℓ} \frac{{(\frac{\partial ℓ}{\partial h})}_{g}}{{(\frac{\partial ℓ}{\partial g})}_{h}}] d h + [{(\frac{d f}{d ℓ})}_{g h} + \frac{{(\frac{\partial f}{\partial g})}_{h ℓ}}{{(\frac{\partial ℓ}{\partial g})}_{h}}] d ℓ$ .

So, we need $g (h, ℓ)$ . From the second EOS, $g = h - \exp (ℓ - h^{2})$ .

Two

Show $\frac{U}{N} = f (T)$ independent of volume from ideal gas law $p V = N k T$ . I.e. show $U \propto N k f (T)$ . If $U (T, V)$ then $d U = \partial_{T} U d T + \partial_{V} U d V$ . So we must show $\partial_{V} U = 0$ . Then, we have $d U = T d S - p d V$ . So, we have $U (S, V)$ so we need $S (T, V)$ to get $U (T, V)$ . Then, $d S = \partial_{T} S d T + \partial_{V} S d V$ . Hence, $d U = T \partial_{T} S d T + T \partial_{V} S d V - p d V$ . So, we must show $T \partial_{V} S - p = 0$ . Now, we must find a Maxwell relation. We have $V, T$ . We have $U (S, V, N)$ , $F (T, V, N)$ , and $H (S, p, N)$ . So we use the free energy $F$ . This gives us, $d F = - S d T - p d V$ . $\partial_{V} S = - \partial_{V} \partial_{T} F = - \partial_{T} \partial_{V} F = \partial_{T} p$ . Then, $T \partial_{T} p - p = 0$ . So, $T \frac{N k}{V} - \frac{N k T}{V} = 0$ , we have achieved what we needed!

A much Simpler Proof

$F = U - T S$ , $d F = - S d T - p d V$ . Then, $- p = \partial_{V} F_{T} = \partial_{V} (U - T S)_{T} = \partial_{V} U_{T} - \partial_{V} (T S)_{T}$ then we get $\partial_{V_{T}} = - T \partial S_{V_{T}}$ .

V,T	p,T
$δ F \leq 0$	$δ G \leq 0$
$\sum δ U_{i} = 0$	$\sum δ H_{i} = 0$

Stability Conditions

Small perturbations do not give large changes instead they give small changes.

Example

Mechanics Example (1D)

Let $U (x)$ be a function of position. Thus, $F = - \frac{\partial U}{\partial x}$ . At equilibrium states, $F = - \frac{\partial U}{\partial x} = 0$ .

At the global minimum, the state is called stable. At a local minumum the state is metastable. At a maximum, the equilibrium is unstable.

Stability is the second order condition, $\frac{\partial^{2} U}{\partial x^{2}} > 0$ .

If we have more than a single coordinate, then $\sum_{i, j} \frac{\partial^{2} U}{\partial x_{i} \partial x_{j}} δ x_{i} δ x_{j} > 0$ .

If we go to a generalized force $j_{i} = \frac{\partial U}{\partial x_{i}}$ then we can make a perturbation in the generalized force $δ j_{i} = δ (\frac{\partial U}{\partial x_{i}}) = \sum_{j} \frac{\partial U}{\partial x_{j} \partial x_{i}} δ x_{j}$ . This gives us the condition, $\sum_{i} δ j_{i} δ x_{i} > 0$ where $x_{i}$ is a generalized displacement. We then see that $δ T δ S + \sum_{i} δ j_{i} δ x_{i} + \sum_{α} δ μ_{a} δ N_{a} > 0$ . And so $δ T δ S - δ p δ V + δ μ δ N > 0$ .

Euler Relation

Extensivity

$U (S, V, N)$ with $U, S, V, N$ are extensive. Mathematically, $λ U (S, V, N) = U (λ S, λ V, λ N)$ . This is also referenced as U is a homogeneous function of order 1. Then, $\frac{\partial}{\partial λ}$ on both sides and then set $λ = 1$ .

$U (S, V, N) = \frac{\partial}{\partial λ} U (λ S, λ V, λ N) = \frac{\partial λ S}{\partial λ} \frac{\partial U}{\partial λ S} + \dots$

From Before

$δ T δ S + δ j δ x + δ μ δ N \geq 0$

How to use? Variations $δ T, δ x$ and, $δ N = 0$ .

$δ S (δ T, δ x), δ J (δ T, δ x)$ .

$δ S = {(\frac{\partial S}{\partial T})}_{x} δ T + {(\frac{\partial S}{\partial x})}_{T} δ x$ $δ j = {(\frac{\partial j}{\partial T})}_{x} δ T + {(\frac{\partial j}{\partial x})}_{T} δ x$

From the original inequality, ${(\frac{\partial S}{\partial T})}_{x} (δ T)^{2} + {(\frac{\partial S}{\partial x})}_{T} δ x δ T + {(\frac{\partial j}{\partial x})}_{T} (δ x)^{2} + {(\frac{\partial j}{\partial T})}_{x} δ T δ x \geq 0$ .

Helmholtz: $F (T, V), d F = - S d T - p d V$ .

Consider the Maxwell relations from the Helmholtz free energy, $d F = - S d T + j d x$ $\frac{\partial^{2} F}{\partial T \partial X} \Rightarrow {(\frac{\partial S}{\partial x})}_{T} = - {(\frac{\partial j}{\partial T})}_{x}$ .

So, ${(\frac{\partial S}{\partial T})}_{x} (δ T)^{2} + {(\frac{\partial j}{\partial x})}_{T} (δ x)^{2} \geq 0$ .

Then, $δ x = 0$ implies that ${(\frac{\partial S}{\partial T})}_{x} = \frac{C_{x}}{T} \geq 0$ . Therefore, the constant volume/ length heat capacity must be non-negative.

Or, $δ T = 0$ implies that ${(\frac{\partial j}{\partial x})}_{T} \geq 0 \Rightarrow κ_{T} = - \frac{1}{V} {(\frac{\partial V}{\partial p})}_{T} \geq 0$ . Therefore the constant temperature heat capacity must be non-negative.

If you have multiple particles, terms will appear in a similar fashion, and you will always have the $(δ T)^{2}$ term. Specifically, if you have more than 1 $J_{i}, x_{i}$ and include $S, T$ in list of $(J_{i}, x_{i})$ . Then, the coefficients $\cdot {(\frac{\partial J_{i}}{\partial x_{j}})}_{i \neq j}$ . The matrix of coefficients must be positive definite. This implies that all eigenvalues are positive and all subdeterminants are positive.

Example: $(p, - V), (μ, N)$ at a constant $T, N$ , $(\begin{matrix} - {(\frac{\partial p}{\partial V})}_{T, N} & {(\frac{\partial p}{\partial N})}_{T, V} - {(\frac{\partial μ}{\partial V})}_{T, N} & - {(\frac{\partial μ}{\partial T})}_{T, V} \end{matrix})$

$κ_{T, N} = - \frac{1}{V} (\frac{\partial V}{\partial P}) T, N > 0$ . ${(\frac{\partial N}{\partial μ})}_{T, V} > 0$ . $- {(\frac{\partial p}{\partial V})}_{T, N} {(\frac{\partial μ}{\partial N})}_{T, V} + {(\frac{\partial p}{\partial N})}_{T, V} {(\frac{\partial μ}{\partial V})}_{T, N} > 0$ .

Consider $G (p, T) = U - T S + p V$ , take $N$ to be constant and consider $T_{0}, p_{0}$ fixed by environment. So, $G (p, T) = U - T_{0} S + p_{0} V$ . Then, $δ G (δ S, δ V) = {(\frac{\partial G}{\partial S})}_{V} δ V + {(\frac{\partial G}{\partial V})}_{S} δ V + \frac{1}{2} {(\frac{\partial^{2} G}{\partial S^{2}})}_{V} (δ S)^{2} + \frac{1}{2} {(\frac{\partial^{2} G}{\partial V^{2}})}_{S} (δ V)^{2} + \frac{\partial^{2} G}{\partial S \partial V} δ S δ V = [{(\frac{\partial U}{\partial S})}_{V} - T_{0}] δ S + [{(\frac{\partial U}{\partial V})}_{S} + p_{0}] δ V + {(\frac{\partial^{2} U}{\partial S^{2}})}_{V} (δ S)^{2} + 2 (\frac{\partial^{2} U}{\partial S \partial V}) δ S δ V + {(\frac{\partial^{2} U}{\partial V^{2}})}_{S} (δ V)^{2} > 0$ . If $δ S, δ V$ are independent then.

For $δ V = 0$ , ${(\frac{\partial^{2} U}{\partial S^{2}})}_{V} = {(\frac{\partial T}{\partial S})}_{V} = \frac{T}{C_{V}} > 0$ . For $δ S = 0$ , ${(\frac{\partial^{2} U}{\partial V^{2}})}_{S} = \frac{1}{V κ_{S}} = - \frac{V}{V} {(\frac{\partial p}{\partial V})}_{S} > 0$ .

Analyzing like a quadratic form, $a x^{2} - f 2 b x; x_{2} + c x_{2}^{2} - > 0$ , ${\overset{―}{x}}^{T} A \overset{―}{a} + b^{T} \overset{―}{x} \geq 1$ . $A = (\begin{matrix} a & b c & d \end{matrix})$ .

So, ${(\frac{\partial^{2} U}{\partial S^{2}})}_{V} {(\frac{\partial^{2} U}{\partial V^{2}})}_{S} - (\frac{\partial^{2} U}{\partial S \partial V}) > 0$ so $\frac{1}{V κ_{S} C_{V}} > {(\frac{\partial T}{\partial V})}_{S}^{2}$ .

Example: Consider a simple substance (one chemical composition) observe 3 phases, $(s, ℓ, g)$ . 20230111105947-thermodynamics.org_20230127_114137.png

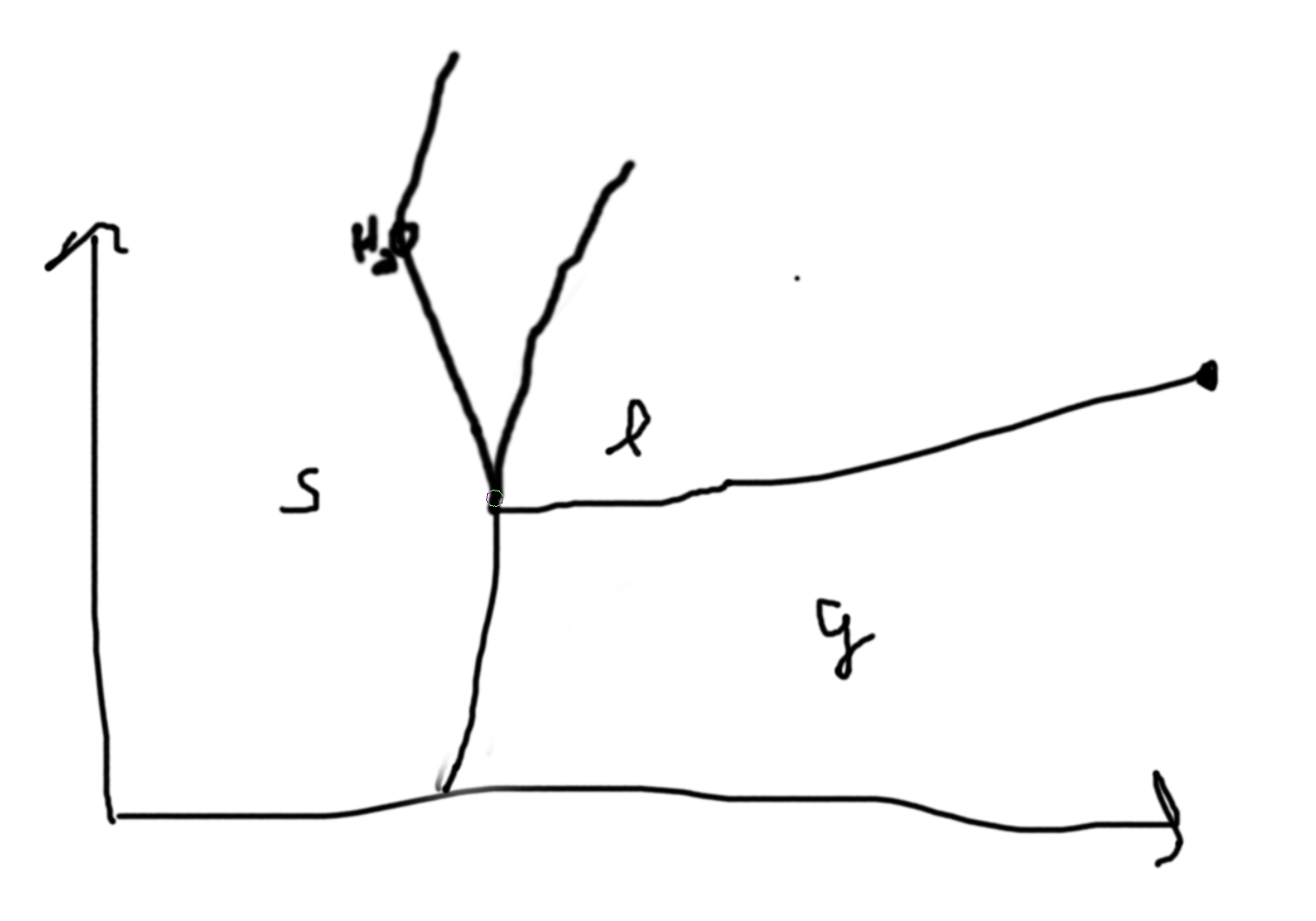
On the lines, we have coexistence of the phases, at intersections we have coexistence of all the phases. Phase boundaries.

20230111105947-thermodynamics.org_20230127_114644.png